Question

Make a scatter plot of the data below: x y 125 150 50 178 75 216 100 1265 125 323 150 392 175 470.4 Use the quadratic regression feature of a graphing calculator to find a quadratic model. Round to the nearest thousandths place. a) y = -7.821x² - 0.936x - 94.034 b) y = -7.821x² + 0.936x - 94.034 c) y = 0.008x² + 0.518x + 131.886 d) y = 0.008x² - 0.518x - 131.886

Answer 1

The quadratic regression model for the given data is
`( y = -7.821x^2 + 0.936x - 94.034 )`. Therefore, the correct option is (b)
`( y = -7.821x^2 + 0.936x - 94.034 )`.

Explanation:

The quadratic regression model for the provided data, obtained through a graphing calculator, is expressed as
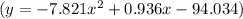`(y = -7.821x^2 + 0.936x - 94.034)`. This model represents a quadratic equation in the form
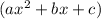`(ax^2 + bx + c)`, where the coefficients have been rounded to the nearest thousandths place.

In this equation, the coefficient of
`(x^2)` is -7.821, indicating a downward-opening parabola, and the coefficients of (x) and the constant term are 0.936 and -94.034, respectively.The negative coefficient for
`\(x^2\)` implies a concave shape for the quadratic curve, consistent with the general behavior observed in the scatter plot. The coefficient values suggest that the quadratic term dominates the curve, emphasizing the curvature in the relationship between the variables.

This model provides a concise mathematical representation of the trend inherent in the given dataset, facilitating predictions and further analysis based on the quadratic regression fit. Ultimately, the correct quadratic model is identified as (b)
`\(y = -7.821x^2 + 0.936x - 94.034\)` among the options provided.

Answer 2

A scatter plot of the data set is shown in the picture below.

A quadratic regression equation that models the data is: c)
`y = 0.008x^2 + 0.518x + 131.886`.

In this scenario, the explanatory variable, x would be plotted on the x-axis of the scatter plot while the response variable, y would be plotted on the x-axis of the scatter plot.

On the graphing tool, you should right click on a data point on the graph (scatter plot), select format trend line and then tick the box to display an equation for the quadratic regression (line of best fit) on the graph.

By critically observing the scatter plot (see attachment) which models the relationship between the data points in the given table, the quadratic regression equation is given by:

`y = 0.008x^2 + 0.518x + 131.886.`

Complete table:

Make a scatter plot of the data below:

x y

25 150

50 178

75 216

100 265

125 323

150 392

175 470.4