Question

Given the function and a domain, find the range.

9) f(x) = -7x+3, D={-12, -4, 3, 20}
10) f(x) = 4x-1, D={xlx}
11) f(x) = 2x² - 2x + 5, D={-2, -1, 0, 1, 2) 12) f(x) = 2x² - 6x +11, D={xlx}​

Answer 1

I'll do problem 9 to get you started.

The domain for problem 9 is the set D = {-12, -4, 3, 20}. These are the only allowed x inputs.

Plug each of them into f(x) to find the corresponding output in the range.

For instance, x = -12 gets us:

`f(\text{x}) = -7\text{x}+3\\\\f(-12) = -7(-12)+3\\\\f(-12) = 84+3\\\\f(-12) = 87\\\\`

The input x = -12 in the domain leads to y = f(x) = 87 in the range.

If we tried x = -4, then,

`f(\text{x}) = -7\text{x}+3\\\\f(-4) = -7(-4)+3\\\\f(-4) = 28+3\\\\f(-4) = 31\\\\`

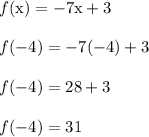
Repeat for x = 3 and x = 20 to get f(3) = -18 and f(20) = -137

The range for problem 9 is the set {87, 31, -18, -137}

I didn't sort the values from smallest to largest because I wanted them to be aligned with the domain values. Eg: 31 is the second value in the unsorted range as it pairs up with -4 as the second item in the domain.