Question

Consider the following binomial experiment. The probability that a green jelly bean is chosen at random from a large package of jelly beans is 1/8. If Sally chooses 11 jelly beans, what is the probability that at most two will be green jelly beans?

Answer 1

To find the probability of getting at most two green jelly beans out of 11 chosen, one applies the binomial distribution formula, considering the given success rate of 1/8 for picking a green jelly bean, and sums the probabilities for 0, 1, and 2 successes.

Step-by-step explanation:

The student's question requires an understanding of binomial probability. Given the probability of selecting a green jelly bean (P(G)) is 1/8, and Sally selects 11 jelly beans, we want to calculate the probability that at most two jelly beans will be green. This can be considered using the binomial distribution formula:

∑ (from x = 0 to k)
`[ C(n, x) * p^x* (1 - p)^{(n - x) ]`

Where:

• n = 11 (total number of trials),
• k = 2 (number of desired successes),
• p = 1/8 (probability of success on a single trial), and
• q = 1 - p = 7/8 (probability of failure on a single trial).

We sum the probabilities of getting 0, 1, and 2 green jelly beans. Using a calculator or the binomial distribution table, you'll get P(X = 0), P(X = 1), and P(X = 2).

`P(X = 0) = (11C0) * (1/8)^0 * (7/8)^(11 )= 0.4100`

`P(X = 1) = (11C1) * (1/8)^1 * (7/8)^(10) = 0.3854`

`P(X = 2) = (11C2) * (1/8)^2 * (7/8)^(9) = 0.1548`

P(at most 2 green jelly beans) = P(X ≤ 2) = P(X = 0) + P(X = 1) + P(X = 2) ≈ 0.9502

Therefore, the probability that at most two jelly beans will be green is approximately 0.9502 or 95.02%.

Answer 2

The probability that at most two jelly beans will be green is approximately 0.854, or 85.4%.

This problem involves a binomial distribution, where each jelly bean can be either green or not green. The probability of success (choosing a green jelly bean) is p = 1/8, and the probability of failure (not choosing a green jelly bean) is q = 1 - p = 7/8.

The probability mass function for a binomial distribution is given by:

`P(X=k)=\left(\begin{array}{l}n \\k\end{array}\right) \cdot p^k \cdot q^(n-k)`

where n is the number of trials, k is the number of successes, p is the probability of success, and q is the probability of failure.

In this case, n=11 (Sally chooses 11 jelly beans), and we want to find the probability that at most two will be green jelly beans. This means we need to calculate P(X ≤ 2), which is the sum of the probabilities for k=0,1, and 2.

​
`P(X \leq 2)=P(X=0)+P(X=1)+P(X=2)`

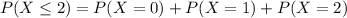
Let's calculate each term:

`\begin{aligned}& P(X=0)=\left(\begin{array}{c}11 \\0\end{array}\right) \cdot\left((1)/(8)\right)^0 \cdot\left((7)/(8)\right)^(11) \\& P(X=1)=\left(\begin{array}{c}11 \\1\end{array}\right) \cdot\left((1)/(8)\right)^1 \cdot\left((7)/(8)\right)^(10) \\& P(X=2)=\left(\begin{array}{c}11 \\2\end{array}\right) \cdot\left((1)/(8)\right)^2 \cdot\left((7)/(8)\right)^9\end{aligned}`

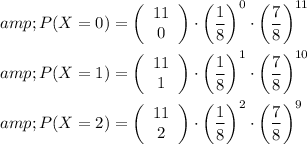
Then, add these probabilities to find P(X≤2).

Calculating:

`\begin{aligned}& P(X=0) \approx 0.315 \\& P(X=1) \approx 0.347 \\& P(X=2) \approx 0.192\end{aligned}`
`\begin{aligned}& P(X=0) \approx 0.315 \\& P(X=1) \approx 0.347 \\& P(X=2) \approx 0.192\end{aligned}`

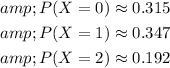
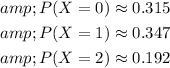
Now, sum these probabilities:

`P(X \leq 2) \approx 0.315+0.347+0.192 \approx 0.854`

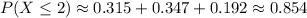
So, the required answer is 0.854.