Answer:
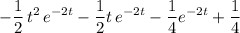 .
.
Step-by-step explanation:
Distance travelled can be found by integrating speed, which is the absolute value (magnitude) of velocity. Since the value of velocity in this question is non-negative over the given range, the expression for speed would be the same as that for velocity:
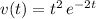 .
.
The distance travelled during the given time would be equal to the definite integral:
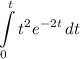 .
.
To find the value of this definite integral, start by integrating
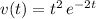 indefinitely using integration by parts.
indefinitely using integration by parts.
In integration by parts:
 ,
,
Where:
 and
and
 are two functions of
are two functions of
 , and
, and
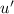 and
and
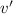 denote the first derivative of
denote the first derivative of
 and
and
 with respect to
with respect to
 .
.
Using the LIATE rule, set
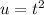 (algebraic) and
(algebraic) and
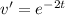 (exponential,) such that
(exponential,) such that
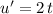 and
and
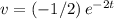 (the constant of integration is omitted here.) Hence:
(the constant of integration is omitted here.) Hence:
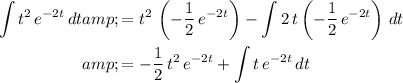 .
.
Similarly, apply integration by parts to integrate
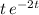 . Set
. Set
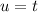 (algebraic) and
(algebraic) and
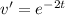 (exponential,) such that
(exponential,) such that
 and
and
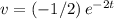 . Using integration by parts:
. Using integration by parts:
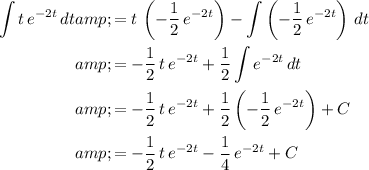 ,
,
Where
 is a constant of integration.
is a constant of integration.
Substitute this result into the previous one:
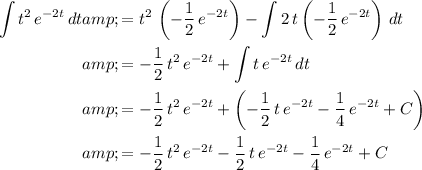 .
.
Evaluate the definite integral for displacement using this result:
![\begin{aligned} &\int \limits_(0)^(t) t^(2) e^(-2 t)\, dt\\ =\; & \left[-(1)/(2)\, t^(2)\, e^(-2 t) -(1)/(2)\, t \, e^(-2 t) -(1)/(4)\, e^(-2 t)\right]^(t)_(0) \\ =\; & \left(-(1)/(2)\, t^(2)\, e^(-2 t) -(1)/(2)\, t \, e^(-2 t) -(1)/(4)\, e^(-2 t)\right) - \left(-(1)/(4)\right) \end{aligned}](https://img.qammunity.org/2024/formulas/physics/high-school/s25aa64q6uhkwetnz7ql6eeypeou3fwd39.png) .
.