Question

A surveyor is tracking the elevation of a trail at fixed increments of 500

meters. The plot in the DE-plane shows the elevation, E, in meters (m)
above the starting point versus the distance, D, along the trail from the
start in kilometers (km). What is the average rate of change in elevation
with respect to distance along the trail in m/km between the starting
point and the point of highest elevation?

Answer 1

20 m/km

Explanation:

average rate of change = f(b)-f(a)/b-a

= 130-0/6.5-0 = 20

hope this helps <3

Answer 2

20 m/km

Explanation:

The average rate of change in elevation with respect to distance along the trail can be calculated using the formula:

`\text{Average Rate of Change} = \frac{\text{Change in Elevation}}{\text{Change in Distance}}`

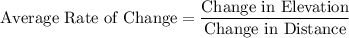
From observation of the graph:

• Starting point = (0, 0)
• Point of highest elevation = (6.5, 130)

The change in elevation is the difference between the y-values of the point of highest elevation and the starting point:

`\rm Change\;in\;elevation=130\;m-0\;m=130\;m`

The change in distance is the difference between the x-values of the point of highest elevation and the starting point:

`\rm Change\;in\;distance=6.5\;km-0\;km=130\;km`

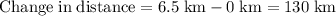
Substitute these values into the formula:

`\text{Average Rate of Change} = (130)/(6.5) \; \text{m/km}`

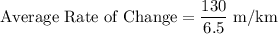
Simplifying the division:

`\text{Average Rate of Change} = 20 \, \text{m/km}`

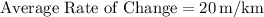
So, the average rate of change in elevation with respect to distance along the trail between the starting point and the point of highest elevation is 20 m/km. This means that for every kilometer along the trail, the elevation increases by an average of 20 meters.