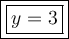Question

Answer just the first part of the question

Solve the equation.
) i)3^(2x )-3^(x+2 )-3^(1+x )=27

Answer 1

`\textsf{(i)} \quad x =(\ln(6 +3√(7)))/(\ln (3))`

`\textsf{(ii)} \quad y=3`

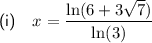
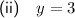
Explanation:

Question (i)

Given equation:

`3^(2x)-3^(x+2)-3^(1+x)=27`

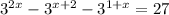
Apply exponent rules to rewrite each term on the left side of the equation in terms of
`3^x`:

`(3^x)^2-3^(x)\cdot 3^(2)-3^(1)\cdot 3^(x)=27`

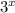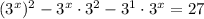
Factor out
`3^x`:

`(3^x)^2-3^(x)(3^(2)+3^(1))=27`

`(3^x)^2-3^(x)(12})=27`

`\textsf{Substitute\;$u = 3^x$:}`

`u^2-12u=27`

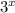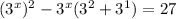
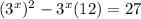
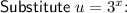
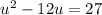
Subtract 27 from both sides to create a quadratic equation in the form ax² + bx + c = 0:

`u^2-12u-27=0`

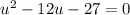
Solve the equation for u using the quadratic formula.

`\boxed{\begin{array}{c}\underline{\sf Quadratic\;Formula}\\\\x=(-b \pm √(b^2-4ac))/(2a)\\\\\textsf{when}\;ax^2+bx+c=0\\\end{array}}`

In this case:

• a = 1
• b = -12
• c = -27

Therefore:

`u=(-(-12) \pm √((-12)^2-4(1)(-27)))/(2(1))`

`u=(12 \pm √(144+108))/(2)`

`u=(12 \pm √(252))/(2)`

`u=(12 \pm 6 √(7))/(2)`

`u=6 \pm 3√(7)`

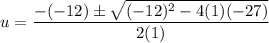
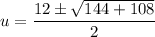
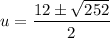
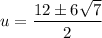
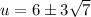
Substitute back
`u = 3^x` and solve for x.

Solution 1

`3^x=6 +3√(7)`

`\ln (3^x)=\ln(6 +3√(7))`

`x \ln (3)=\ln(6 +3√(7))`

`x =(\ln(6 +3√(7)))/(\ln (3))`

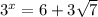
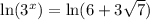
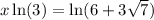
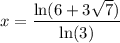
Solution 2

`3^x=6 -3√(7)`

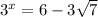
As
`6 - 3√(7) < 0`, and
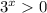`3^x > 0`, there are no solutions for x ∈ R.

Therefore, the only valid solution to the given equation is:

`\large\boxed{\boxed{x =(\ln(6 +3√(7)))/(\ln (3))}}`

`\hrulefill`

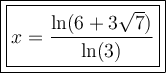
Question (ii)

Given equation:

`2^(2y+1)-15(2^y)=8`

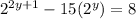
Apply exponent rules to rewrite each term on the left side of the equation in terms of
`2^y`:

`2^(2y)\cdot 2^1-15(2^y)=8`

`(2^(y))^2\cdot 2-15(2^y)=8`

`2(2^(y))^2-15(2^y)=8`

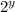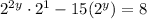
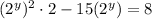
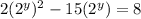
Subtract 8 from both sides:

`2(2^(y))^2-15(2^y)-8=0`

`\textsf{Substitute\;$u = 2^y$:}`

`2u^2-15u-8=0`

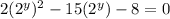
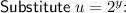
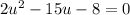
Factor the quadratic equation:

`\begin{aligned}2u^2-16u+u-8&=0\\2u(u-8)+1(u-8)&=0\\(u-8)(2u+1)&=0\end{aligned}`

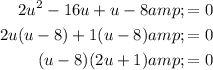
Solve for u:

`u-8=0 \implies u=8`

`2u+1=0 \implies u=-(1)/(2)`

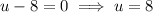
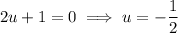
Substitute back
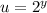`u = 2^y` and solve for y.

Solution 1

`\begin{aligned}2^y&=8\\2^y&=2^3\\y&=3\end{aligned}`

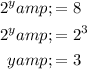
Solution 2

`2^y=-(1)/(2)`

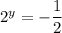
As
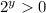`2^y > 0`, there are no solutions for y ∈ R.

Therefore, the only valid solution to the given equation is:

`\large\boxed{\boxed{y=3}}`