Question

If p = 2i + 4j and q = 3i+j, find the magnitude and direction of the resultant of p and q.​

Answer 1

`\textsf{Magnitude:} \quad |\mathbf{R}|=5√(2)`

`\textsf{Direction:} \quad 45^(\circ)`

Explanation:

Given vectors:

`\mathbf{p} = 2\mathbf{i}+ 4\mathbf{j}`

`\mathbf{q} = 3\mathbf{i}+ \mathbf{j}`

The vectors i and j are standard unit vectors, so they each have a length of 1 unit.

• i is in the direction of the positive x-axis.
• j is in the direction of the positive y-axis.

A resultant vector is a single vector that represents the sum of two or more individual vectors. Therefore, the resultant vector R is:

`\begin{aligned}\mathbf{R}=\mathbf{p}+\mathbf{q} &= 2\mathbf{i}+ 4\mathbf{j}+3\mathbf{i}+ \mathbf{j}\\&= 2\mathbf{i}+3\mathbf{i}+ 4\mathbf{j}+ \mathbf{j}\\&= (2+3)\mathbf{i}+ (4+1)\mathbf{j}\\&= 5\mathbf{i}+ 5\mathbf{j}\end{aligned}`

The magnitude of a vector is a scalar value that represents the length of the vector. It is the distance between the vector's start point and end point.

The formula for the magnitude of vector a = xi + yj is:

`|\mathbf{a}|=√(x^2+y^2)`

Therefore, the magnitude of resultant vector R is:

`\begin{aligned}|\mathbf{R}|&=√(5^2+5^2)\\&=√(25+25)\\&=√(50)\\&=√(5^2\cdot 2)\\&=√(5^2)√(2)\\&=5√(2)\end{aligned}`

The direction of a vector a = xi + yj is the angle θ between a line parallel to the x-axis and a, where 0° ≤ θ < 360°. It is measured anticlockwise from the positive x-axis. So, the direction of the vector can be found using the tangent trigonometric ratio:

`\tan \theta=(y)/(x)`

Therefore, the direction of the resultant vector R = 5i + 5j is:

`\begin{aligned}\tan \theta&=(5)/(5)\\\\\tan \theta&=1\\\\\theta&=\tan ^(-1)(1)\\\\\theta&=45^(\circ)\end{aligned}`

In conclusion, the magnitude of the resultant vector is 5√2, and its direction is 45° (anticlockwise from the positive x-axis).

Answer 2

The magnitude of the resultant vector = 7.07 units

The direction of the resultant vector = 45°

Explanation:

Note:

The length of the vector that represents the sum of two or more vectors is known as the magnitude of the resultant.

Likewise, the angle that the resultant vector makes with a reference direction is referred to as the direction of the resultant.

if we have two vectors, A and B, the magnitude of the resultant vector, R, is given by:

`\sf R = √(A^2 + B^2)`

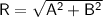
where A and B are the magnitudes of vectors A and B.

The direction of the resultant vector, R, is given by:

`\sf Tan(\theta) =(B)/(A)`

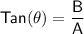
where θ is the angle that the resultant vector makes with the reference direction.

`\hrulefill`

For the Question:

Given vectors:

P = 2i + 4j

Q = 3i + j

Calculate the resultant vector of R:
R = P + Q:

R = (2i + 4j) + (3i + j)

R = 2i + 4j + 3i + j

R = (2 + 3)i + (4 + 1)j

R = 5i + 5j

Find the magnitude of R:

`\sf |R| = √((5i)^2+ (5j)^2)`

`\sf |R| = √(25+ 25)`

`\sf |R| = √(50)`

`\sf |R| = 5√(2)`

`\sf |R| \approx 7.07`

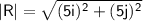
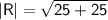
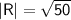
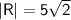
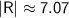
Find the direction of R:

`\sf Tan \theta =(Ry )/( Rx)`

`\sf Tan \theta = (5)/(5)`

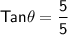
We can use the inverse tangent function to find the value of θ.

`\sf \theta = Tan^(-1) (1)`

`\sf \theta = 45^\circ`

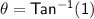
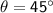
So, the magnitude of the resultant vector is 7.07 units, and the direction of the resultant vector is 45° with respect to the positive x-axis.