Question

Which graph shows the system startlayout enlarged left-brace 1st row x squared y = 2 2nd row x squared y squared = 9 endlayout? on a coordinate plane, a graph of a circle and a parabola are shown. the circle has a center at (0, 0) and a radius of 3 units. the parabola opens down and intersects the circle at (negative 2, negative 2), has a vertex at (0, 2), and intersect the circle again at (2, negative 2). on a coordinate plane, a graph of a circle and a parabola are shown. the circle has a center at (0, 0) and a radius of 3 units. the parabola opens up and intersects the circle at (negative 2, 2), has a vertex at (0, negative 2), and intersect the circle again at (2, 2). on a coordinate plane, a graph of a circle and a parabola are shown. the circle has a center at (0, 3) and has a radius of 3 units. the parabola opens up and intersects the circle at (negative 2, 5), has a vertex at (0, 2), and intersects the circle again at (2, 5). on a coordinate plane, a graph of a circle and a parabola are shown. the circle has a center at (0, 3) and has a radius of 3 units. the parabola opens down and goes through (negative 2, negative 2), has a vertex at (0, 2), and goes through (2, negative 2).

Answer 1

The correct in option is: 4

1.
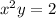`\(x^2y = 2\)` (parabola, opens up)

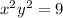`\(x^2y^2 = 9\)` (circle, center at (0, 0), radius 3)

Parabola intersects the circle at (-2, 2), (0, -2), and (2, 2).

The given conditions are satisfied for the parabola and circle.

2.
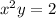`\(x^2y = 2\)` (parabola, opens down)

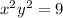`\(x^2y^2 = 9\)` (circle, center at (0, 0), radius 3)

Parabola intersects the circle at (-2, -2), (0, 2), and (2, -2).

The given conditions are satisfied for the parabola and circle.

3.
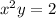`\(x^2y = 2\)` (parabola, opens up)

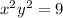`\(x^2y^2 = 9\)` (circle, center at (0, 3), radius 3)

Parabola intersects the circle at (-2, 5), (0, 2), and (2, 5).

The given conditions are not satisfied, as the parabola's vertex is at (0, 2) and not (0, 3).

4.
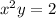`\(x^2y = 2\)` (parabola, opens down)

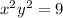`\(x^2y^2 = 9\)` (circle, center at (0, 3), radius 3)

Parabola intersects the circle at (-2, -2), (0, 2), and (2, -2).

The given conditions are satisfied for the parabola and circle.

Based on the analysis, the correct graph is described in option 4:
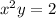`\(x^2y = 2\)` (parabola, opens down) and
`\(x^2y^2 = 9\)`

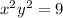
(circle, center at (0, 3), radius 3).