Question

Given: δmno prove: the medians of δmno are concurrent. which reason completes the proof for step 6?

Answer 1

Definition of midpoint

Explanation:

Midpoint formula:

(
`x_(1)` +
`x_(2)`)/2 (
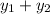`y_(1)+y_(2)`)/2

Let P' be the midpoint of M'(0, 0) N'(2r, 2s):

(0 + 2r)/2 = r & (0 + 2s)/2 = s

Thus, P' = (r,s)

Let Q' be the midpoint of O'(2t,0) N'(2r, 2s):

(2t+2r)/2=t + r & (0+2s)/2 = s

Thus, Q' = (t + r, s)

Let R' be the midpoint of M' (0, 0) O'(2t,0):

(O + 2t)/2 = t & (0 + 0)/2 = 0

Thus, R' = (t, 0)

Since step 6 of the proof is P' = (r,s), Q' = (t + r, s), R' = (t, 0), which is true when the midpoint formula is applied, the answer is "Definition of midpoint"

Answer 2

The statement missing in 6 is the medians are concurrent.

What is median in geometry?

In geometry, the median of a triangle is a line segment connecting a vertex to the midpoint of the opposite side.

Given ∆PQR whose medians are M'Q', N'R' and O'P'

To prove that 'Three medians of a triangle are concurrent'.

Given that the point of intersection S is

`s = (( - 2)/(3)(r + t) \: \: ( - 2)/(3)s)`

Also given is the equation of the median

`y = (s)/(2t - r)x - (2st)/(2t - r)`

Substitute the y-value in point S to the equation.

`( - 2)/(3)s = (s)/(2t - r)x - (2st)/(2t - r)`

`( - 2)/(3)s = (s)/(2t - r)( ( - 2r - 2t)/(3)) - (2st)/(2t - r)`

Simplify the equation

`( - 2)/(3)s = ( - 2)/(3)s`

The coordinates of point S is a solution to the equation of the median y(x).

The statement missing in 6 is the medians are concurrent.

Complete question