Question

An exponential function follows a pattern of decay through the points (–2, 25), (–1, 5), and (0, 1). Determine the base of the function.

5
–5
negative one fifth
one fifth

Answer 1

The base, 'b', of the exponential function is 1/5.

`\displaystyle f(x)=\Big((1)/(5)\Big)^x`

Explanation:

The question asks us to determine the base of an exponential decay function that passes through the points (–2, 25), (–1, 5), and (0, 1). To solve this, we will identify the general form of an exponential decay function, substitute the given points into the function to establish equations, and then solve for the unknown base.

`\hrulefill`

The general form of an exponential function is:

`\boxed{\left\begin{array}{ccc}\text{\underline{Exponential Function:}}\\\\f(x)=ab^x\\\\\text{Where:}\\\bullet \ a \ \text{is the initial value}\\\bullet \ b \ \text{is the base}\\\bullet \ x \ \text{is the exponent}\end{array}\right}`

Since the function passes through the point (0, 1) and we know that f(0) = 1. Substituting these into f(x)=abˣ:

`\Longrightarrow 1=ab^0\\\\\\\\\Longrightarrow 1=a(1)\\\\\\\\\therefore a=1`

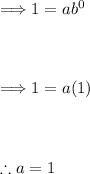
Now we can rewrite our general equation:

`\Longrightarrow f(x)=b^x`

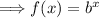
Next, we'll use the points (–1, 5) and (–2, 25) to find 'b'.

From f(−1) = 5, we get:

`\Longrightarrow 5=b^(-1)\\\\\\\\\therefore 5 = (1)/(b)`

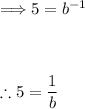
From f(−2) = 25, we get:

`\Longrightarrow 25=b^(-2)\\\\\\\\\therefore 25 = (1)/(b^2)`

To find 'b', we can solve either of these equations. Let's use the first equation:

`\Longrightarrow 5 = (1)/(b)\\\\\\\\\therefore \boxed{\boxed{b=(1)/(5)}}`

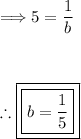
We can check that this value of 'b' also satisfies the second equation:

`\Longrightarrow 25 = (1)/(b^2)\\\\\\\\\Longrightarrow 25 = (1)/(((1)/(5) )^2)\\\\\\\\\Longrightarrow 25 = (1)/(1/25)\\\\\\\\\therefore 25=25`

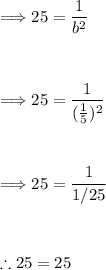
The equations are consistent, confirming that the base 'b' of the exponential decay function is 1/5.