Question

Select the first five terms of the sequence defined recursively. a_(1)=27,a_(k+1)=a_(k)+4

Answer 1

Answer: 27, 31, 35, 39, 43

Step-by-step explanation

The notation a_(k+1)=a_(k)+4 can also be written as
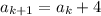`a_(k+1) = a_k + 4` where the "k+1" and "k" are subscripts.

Let's plug in k = 1

`a_(k+1) = a_k + 4\\\\a_(1+1) = a_1 + 4\\\\a_2 = a_1 + 4\\\\a_2 = 27 + 4\\\\a_2 = 31`

We add 4 to the previous term to get the next term.

Repeat for k = 2

`a_(k+1) = a_k + 4\\\\a_(2+1) = a_2 + 4\\\\a_3 = a_2 + 4\\\\a_3 = 31 + 4\\\\a_3 = 35`

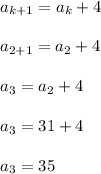
Keep going for k = 3 and k = 4. I'll let the student do those set of steps.

After doing so you should get the following

`a_4 = 39\\\\a_5 = 43\\\\`

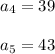
Therefore, the first five terms are: 27, 31, 35, 39, 43.

We add 4 to each term to get the next one. This sequence is arithmetic.