Question

How many zeros does the product $5^3 \times 25^6 \times 3^3 \times 4^7$ end with?

Answer 1

The amount of zeros the product of 5^3 times 25^6 times 3^3 times 4^7 are 14 zeros

Answer 2

14

Explanation:

To find the number of trailing zeros in the product 5³ × 25⁶ × 3³ × 4⁷, we need to consider the prime factorization of each number and their powers.

Rewrite each number so that its base is a prime number.

The base of 5³ is already a prime number.

The prime factorization of 25 is 5².

Therefore, we can rewrite the base of 25⁶ as (5²) and apply the power of a power exponent rule:

`\sf 25^6=(5^2)^6=5^(2 \cdot 6)=5^(12)`

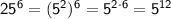
The base of 3³ is already a prime number.

The prime factorization of 4 is 2².

Therefore, we can rewrite the base of 4⁷ as (2²) and apply the power of a power exponent rule:

`\sf 4^7=(2^2)^7=2^(2 \cdot 7)=2^(14)`

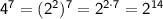
Therefore, the prime factorization of the product is:

`\sf 5^3 * 5^(12) * 3^3* 2^(14)`

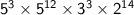
Simplify further by combining the terms with the same base, by applying the product of powers exponent rule:

`\sf 5^(3+12)* 3^3* 2^(14)= 5^(15)* 3^3* 2^(14)`

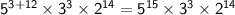
Therefore, the prime factorization of the product is:

`\large\boxed{\sf 2^(14)* 3^3* 5^(15)}`

Trailing zeros within a number result from the presence of the prime factors 2 and 5, which together form the composite factor of 10. So, each pair of 2 and 5 will create a trailing zero.

Therefore, to find the number of trailing zeros in the given product, we need to count the pairs of factors of 2 and 5. In this case, as there are fewer occurrences of the factor 2 compared to the factor 5, the number of trailing zeros is equal to the exponent of base 2. Therefore, there are 14 trailing zeros in the given product.