Question

Write the expression in the standard form a + bi. (9+2i)(6-3i)

Answer 1

Explanation:

54 - 27i + 12i - 6i^2

54 - 15i + 6

60 - 15i

Answer 2

Answer: 60 - 15i

Explanation:

Our task is to multiply the following complex numbers:

• (9 + 2i)(6 - 3i)

The whole idea is that we multiply two complex numbers together just like we multiply any two binomials - using the FOIL method.

FOIL is an acronym that helps us remember how to multiply two binomials. It stands for:

• First
• Outer
• Inner
• Last

Let's see FOIL in action.

We need to multiply these complex numbers:

`\sf{(9+2i)(6-3i)}`

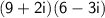
According to FOIL, we should first multiply the first terms.

The first terms are 9 and 6; once we multiply them we get 54.

Then, we should multiply the outer terms, which are 9 and -3i; once we multiply them we get -27i.

Then, we multiply the inner terms, which are 2i and 6; once we multiply them, we get 12i.

Finally, we multiply the last terms, which are 2i and -3i; we get -6i².

As a result, we have: 54 - 27i + 12i - 6i².

Combine like terms:
`\sf{54-15i-6i^2}`

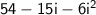
We can actually simplify further; remember that by definition,
`\Large\boxed{\sf{i^2=-1}}`, so, we can simplify a bit further if we plug in -1 instead of i^2.

`\sf{54-15i-6(-1)}`

`\sf{54-15i+6}`

`\sf{60-15i}`

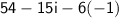
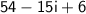
∴ the answer, written in the form a + bi, is 60 - 15i.