Question

Let $g(x)=\sqrt[3]{\frac{x+3}{4}}$. Find the value of $x$ such that $g(2x)=(g(x))^2$.

Answer 1

`x = -1`

`x = 3`

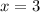
Explanation:

Given:

`g(x)=\sqrt[3]{(x+3)/(4)}`

To find the value of x such that g(2x) = (g(x))², substitute x = 2x into g(x), then equate it to the square of function g(x):

`\begin{aligned}g(2x)&=(g(x))^2\\\\\sqrt[3]{(2x+3)/(4)}&=\left(\sqrt[3]{(x+3)/(4)}\right)^2\end{aligned}`

`\textsf{Apply the exponent rule:} \quad \left(\sqrt[n]{a}\right)^m=a^{(m)/(n)}`

`\left((2x+3)/(4)\right)^(1)/(3)}=\left((x+3)/(4)\right)^(2)/(3)}`

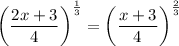
Cube both sides of the equation:

`\left(\left((2x+3)/(4)\right)^(1)/(3)}\right)^3=\left(\left((x+3)/(4)\right)^(2)/(3)}\right)^3`

`\textsf{Apply the exponent rule:} \quad (a^b)^c=a^(bc)`

`\begin{aligned}\left((2x+3)/(4)\right)^(1)&=\left((x+3)/(4)\right)^(2)\\\\(2x+3)/(4)&=\left((x+3)/(4)\right)^(2)\end{aligned}`

`\textsf{Apply the exponent rule:} \quad \left((a)/(b)\right)^c=(a^c)/(b^c)`

`\begin{aligned}(2x+3)/(4)&=((x+3)^2)/(4^2)\\\\(2x+3)/(4)&=((x+3)^2)/(16)\end{aligned}`

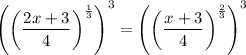
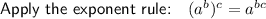
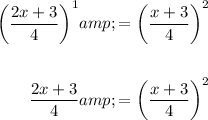
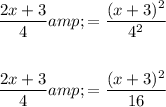
Cross multiply and expand:

`\begin{aligned}16(2x+3)&=4(x+3)^2\\\\32x+48&=4(x^2+6x+9)\end{aligned}`

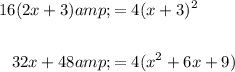
Divide both sides by 4:

`8x+12=x^2+6x+9`

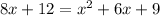
Rearrange to ax² + bx + c = 0 form:

`\begin{aligned}8x+12-8x-12&=x^2+6x+9-8x-12\\\\0&=x^2-2x-3\\\\x^2-2x-3&=0\end{aligned}`

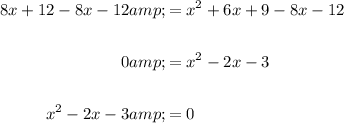
Factor and solve for x:

`\begin{aligned}x^2-3x+x-3&=0\\\\x(x-3)+1(x-3)&=0\\\\(x+1)(x-3)&=0\\\\x+1&=0 \implies x=-1\\x-3&=0 \implies x+3\end{aligned}`

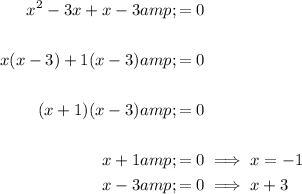
Therefore, the two values of x are x = -1 and x = 3.