Question

Michael made a 4-year investment. The interest rate was 7.5%. After 4 years he earned $2400 in interest. How much was his original investment? Michael's original investment was​

Answer 1

Explanation:

To find Michael's original investment, we can use the formula for simple interest:

Interest = Principal * Interest Rate * Time

In this case, the interest is $2400, the interest rate is 7.5%, and the time is 4 years. Let's substitute these values into the formula and solve for the principal:

$2400 = Principal * 0.075 * 4

Multiplying 0.075 by 4 gives us 0.3:

$2400 = Principal * 0.3

To isolate the principal, we divide both sides of the equation by 0.3:

$2400 / 0.3 = Principal

The result is:

$8000 = Principal

Therefore, Michael's original investment was $8000.

Answer 2

Original investment (annual compound interest) = $7,154.16

Original investment (simple interest) = $8,000

Explanation:

Note: The question does not state whether the interest is compound or simple. Therefore, calculations for both types of interest are given below.

`\hrulefill`

Compound interest

Investment accounts typically use compound interest rather than simple interest. Therefore, assuming Michael invested his money in an account with an annual compound interest rate of 7.5%, we can use the compound interest formula to calculate his original investment.

Compound Interest Formula

`\large\boxed{\sf A=P\left(1+(r)/(n)\right)^(nt)}`

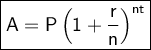
where:

• A = Final amount.
• P = Principal amount invested.
• r = Interest rate (in decimal form).
• n = Number of times interest is applied per year.
• t = Time (in years).

In this case, we know that Michael's investment was for 4 years, the interest rate was 7.5%, and he earned $2400 in interest. We want to find the original investment amount (P).

Therefore, the given values are:

• A = P + interest = P + $2400
• r = 7.5% = 0.075
• n = 1 (compounded annually)
• t = 4 years

Substitute the values into the formula:

`\sf P+2400=P\left(1+(0.075)/(1)\right)^(4)`

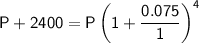
Simplify and solve for P:

`\sf P+2400=P\left(1.075\right)^(4)`

`\sf 2400=P\left(1.075\right)^(4)-P`

`\sf 2400=P(\left(1.075\right)^(4)-1)`

`\sf P=(2400)/(\left(1.075\right)^(4)-1)`

`\sf P=7154.16027...`

`\sf P=\$7154.16`

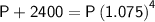
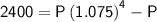
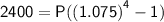
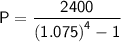
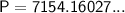
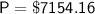
Therefore, if Michael's investment earned annual compound interest, his original investment would be $7,154.16.

`\hrulefill`

Simple interest

If Michael invested his money into an account that uses simple interest, we can use the simple interest formula to calculate his original investment.

Simple Interest Formula

`\large\boxed{\sf I=Prt}`

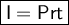
where:

• I = Interest earned.
• P = Principal amount invested.
• r = Interest rate (in decimal form).
• t = Time (in years).

In this case, we know that Michael's investment was for 4 years, the interest rate was 7.5%, and he earned $2400 in interest. We want to find the original investment amount (P).

Therefore, the given values are:

• I = $2400
• r = 7.5% = 0.075
• t = 4 years

Substitute the given values into the formula and solve for P:

`\sf 2400=P\cdot 0.075 \cdot 4`

`\sf 2400=0.3\:P`

`\sf (2400)/(0.3)=(0.3\:P)/(0.3)`

`\sf 8000=P`

`\sf P=8000`

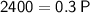
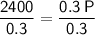
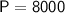
Therefore, if Michael's investment earned simple interest, his original investment would be $8,000.