Answer:
(1)

(2)
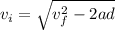
(3)
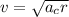
(4)
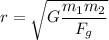
(5)

Step-by-step explanation:
We are given a set of basic physic formulas. We are asked to solve these given literal equations for a certain variable.
What are literal equations?
Literal equations are equations that involve multiple variables, where you're typically solving for one variable in terms of the others. In other words, you manipulate the equation to isolate a specific variable on one side of the equation while the other variables are on the other side.

Question #1:
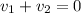 ; solve for 'v₁'
; solve for 'v₁'
Subtract 'v₂' from either side of the equation:
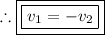
Question #2:
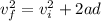 ; solve for 'v_i'
; solve for 'v_i'
Subtract '2ad' from either side of the equation:
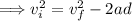
Take the square root of both sides of the equation:
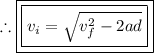
Question #3:
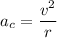 ; solve for 'v'
; solve for 'v'
Multiply each side of the equation by 'r':
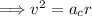
Take the square root of both sides of the equation:
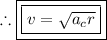
Question #4:
 ; solve for 'r'
; solve for 'r'
Multiply each side of the equation by 'r²':

Divide each side of the equation by 'F_g':
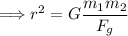
Take the square root of both sides of the equation:
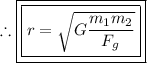
Question #5:
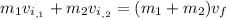 ; solve for 'v_{i,2}'
; solve for 'v_{i,2}'
Subtract 'm₁v_{i,1}' from either side of the equation:
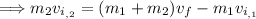
Divide each side of the equation by 'm₂':
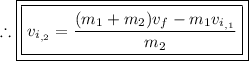
Thus, all parts have been solved.