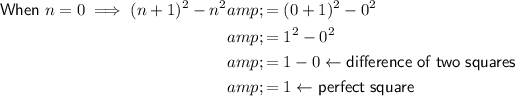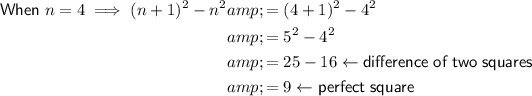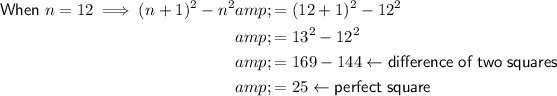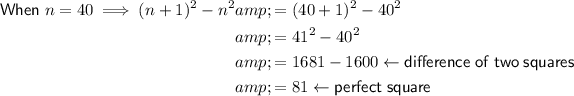Question

Find the number of perfect squares less than $100$ that can be represented as the difference of two consecutive perfect squares.

Answer 1

Five perfect squares: 1, 9, 25, 49 and 81.

Explanation:

A perfect square is a positive integer that can be expressed as the product of an integer multiplied by itself.

Let n² represent a perfect square, where n is an integer.

Therefore, (n + 1)² represents the consecutive (next) perfect square.

So, the difference between two consecutive perfect squares can be modelled as:

`(n + 1)^2 - n^2`

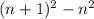
Simplify:

`\begin{aligned}(n + 1)^2 - n^2&=(n+1)(n+1)-n^2\\&=n^2+n+n+1 - n^2\\&=2n+1\end{aligned}`

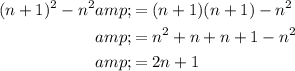
Therefore, 2n + 1 represents the difference between two consecutive perfect squares.

An even number can be represented as 2n (since an even number is divisible by 2). When 1 is added to an even number, it becomes an odd number. Therefore, 2n + 1 represents an odd number.

The perfect squares that are less than 100 are:

• 0, 1, 4, 9, 16, 25, 36, 49, 64, and 81.

Therefore, the odd perfect squares that are less than 100 are:

• 1, 9, 25, 49 and 81.

Therefore, five perfect squares less than 100 can be represented as the difference of two consecutive perfect squares.

`\begin{aligned}\textsf{When}\; n=0 \implies (n+1)^2-n^2&=(0+1)^2-0^2\\&=1^2-0^2\\&=1-0 \leftarrow \sf difference\; of\; two\;squares\\&=1 \leftarrow \sf perfect\;square\end{aligned}`

`\begin{aligned}\textsf{When}\; n=4 \implies (n+1)^2-n^2&=(4+1)^2-4^2\\&=5^2-4^2\\&=25-16 \leftarrow \sf difference\; of\; two\;squares\\&=9 \leftarrow \sf perfect\;square\end{aligned}`

`\begin{aligned}\textsf{When}\; n=12 \implies (n+1)^2-n^2&=(12+1)^2-12^2\\&=13^2-12^2\\&=169-144 \leftarrow \sf difference\; of\; two\;squares\\&=25 \leftarrow \sf perfect\;square\end{aligned}`

`\begin{aligned}\textsf{When}\; n=24 \implies (n+1)^2-n^2&=(24+1)^2-24^2\\&=25^2-24^2\\&=625-576 \leftarrow \sf difference\; of\; two\;squares\\&=49\leftarrow \sf perfect\;square\end{aligned}`

`\begin{aligned}\textsf{When}\; n=40 \implies (n+1)^2-n^2&=(40+1)^2-40^2\\&=41^2-40^2\\&=1681-1600 \leftarrow \sf difference\; of\; two\;squares\\&=81\leftarrow \sf perfect\;square\end{aligned}`