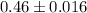The correct option is B.
The confidence interval expressed in the form of
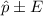 is
is
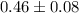 .
.
To express the confidence interval in the form of
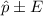 , where
, where
 is the point estimate of the population proportion and
is the point estimate of the population proportion and
 is the margin of error, you would follow these steps:
is the margin of error, you would follow these steps:
A. Calculate the point estimate,
 , which is the midpoint of the confidence interval.
, which is the midpoint of the confidence interval.
B.Calculate the margin of error,
 , which is the difference between the point estimate and either end of the confidence interval.
, which is the difference between the point estimate and either end of the confidence interval.
Given the confidence interval
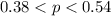 , here's how you would calculate it:
, here's how you would calculate it:
A. Find the midpoint
 :
:
- The midpoint is
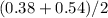 .
.
Certainly, let's go through the steps to calculate the midpoint,
 , which is the point estimate of the population proportion:
, which is the point estimate of the population proportion:
1. Identify the lower and upper bounds of the confidence interval:
- The lower bound is given as
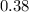 .
. - The upper bound is given as
 .
.
2. Calculate the midpoint
 :
:
- To find the midpoint, you add the lower and upper bounds together and then divide by
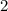 .
. - The formula to calculate the midpoint is
 .
.
3. Apply the values to the formula:
- Substitute the given values into the formula:
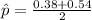 .
.
4. Calculate the midpoint
 :
:
- Perform the addition and division:
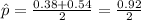 .
.
5. Find the value of
 :
:
- Divide
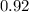 by
by
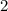 to get the midpoint.
to get the midpoint.
The midpoint calculation step by step is:
![\[\hat{p} = \frac{{0.38 + 0.54}}{2} = \frac{{0.92}}{2} = 0.46\]](https://img.qammunity.org/2024/formulas/mathematics/high-school/twwsd36dqfd9y253hj3ltr2gdw298clcqi.png)
Thus, the midpoint of the confidence interval, which is the point estimate
 , is
, is
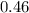 .
.
B. Find the margin of error
 :
:
- The margin of error is
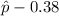 or
or
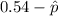 (both should give you the same result since
(both should give you the same result since
 is in the middle).
is in the middle).
To calculate the margin of error
 , you can use either the lower or upper bound of the confidence interval and the point estimate
, you can use either the lower or upper bound of the confidence interval and the point estimate
 . Since the point estimate is the midpoint of the interval, the margin of error will be the same whether you subtract the lower bound from
. Since the point estimate is the midpoint of the interval, the margin of error will be the same whether you subtract the lower bound from
 or subtract
or subtract
 from the upper bound. Here's how you do it step by step:
from the upper bound. Here's how you do it step by step:
1. Identify the point estimate
 :
:
- From the previous step, we found that
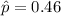 .
.
2. Calculate the margin of error using the lower bound:
- The formula to calculate the margin of error using the lower bound is
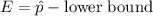 .
.
- Substitute the given values into the formula:
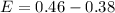 .
.
3. Alternatively, calculate the margin of error using the upper bound:
- The formula to calculate the margin of error using the upper bound is
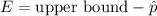 .
. - Substitute the given values into the formula:
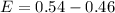 .
.
4. Perform the subtraction to find
 :
:
- Using the lower bound:
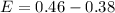 .
. - Using the upper bound:
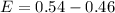 .
.
5. Identify the value of
 :
:
- Both calculations should yield the same result for
 .
.
Let's perform both calculations to confirm that they yield the same margin of error:
The margin of error
 calculated using both the lower and upper bounds is
calculated using both the lower and upper bounds is
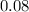 .
.
This confirms that the margin of error is the same whether you use the lower or upper bound because the point estimate
 is the exact midpoint of the interval:
is the exact midpoint of the interval:
- Using the lower bound:

- Using the upper bound:
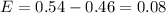
Hence, the margin of error
 is
is
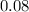 .
.
Let's calculate these values.
The point estimate
 of the population proportion is
of the population proportion is
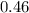 and the margin of error
and the margin of error
 is
is
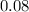 .
.
Therefore, The answer is
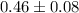 .
.
The complete question is here:
Express the confidence interval
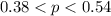 in the form of
in the form of
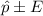 .
.
A.

B.
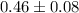
C.
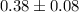
D.