Question

What is the slope of a line that is perpendicular to the line with equation 4x+3y=−54 ?

Answer 1

Answer: The slope is 3/4

Explanation:

Our task is to find the slope of the line that is perpendicular to the one whose equation is
`\sf{4x+3y=-54}`.

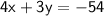First, let's rewrite this equation in slope-intercept form:

`\bullet\qquad\boldsymbol{\sf{y=mx+b}}`

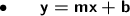
Subtract
`4x` from both sides.

`\sf{3y=-54-4x}`

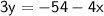
Divide both sides by 3.

`\sf{y=-\cfrac{54}{3}-\cfrac{4}{3}x}`

`\boxed{\boxed{\bf{y=-\cfrac{4}{3}x-18}}}`

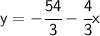
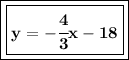
Here's the line's equation. Now, what is the slope of the line that's perpendicular to the one whose equation we just found?

You may recall that perpendicular lines have slopes that are negative inverses of one another. The opposite inverse of -4/3 is 3/4.

Answer 2

perpendicular slope =
`(3)/(4)`

Explanation:

the equation of a line in slope- intercept form is

y = mx + c ( m is the slope and c the y- intercept )

given

4x + 3y = - 54 ( subtract 4x from both sides )

3y = - 4x - 54 ( divide through by 3 )

`(3)/(3)` y =
`(-4)/(3)` x -
`(54)/(3)` , that is

y = -
`(4)/(3)` x - 18 ← in slope- intercept form

with slope m = -
`(4)/(3)`

given a line with slope m then the slope of a line perpendicular to it is

`m_(perpendicular)` = -
`(1)/(m)` = -
`(1)/(-(4)/(3) )` =
`(3)/(4)`