Question

How many squares are exactly four greater than a prime?

Answer 1

Hi,

Explanation:

p is the prime we search.

n² is the square

n²=p+4

n²-4=p

p=(n-2)(n+2)

p being a prime the smallest factor must be 1 else there would be 2 factors greater than 1 for p which would not be a prime.

n-2 =1 => n=3 => n+2=5

n²=9 is the only square responding to the question.

I hope that you understand my poor English.

Answer 2

1

Explanation:

Let
`p` be a prime and
`n` be a positive integer. Then, we need to find all solutions to the equation
`p=n^2-4`.

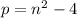Using difference of squares, we rewrite the equation as
`p=(n-2)(n+2)`.

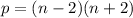Since one of the factors on the right hand side must equal one, we consider
`n=3` and
`n=-1`.

If
`n=-1`, then
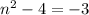`n^2-4=-3`, which is not a prime.

if
`n=3`, then
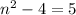`n^2-4=5`, which is a prime.