Question

Find the length of the third side. If necessary, round to the nearest tenth.

Answer 1

16.5

Given :

• Hypotenuse = 21
• Base = 13

To find : Perpendicular

Solution :

By using Pythagoras theorem,

• 
  `Perpendicular = \sqrt{(hypotenuse) {}^(2) - {(base)}^(2) } \\`
• 
  `Perpendicular = \sqrt{(21) {}^(2) - {(13)}^(2) } \\`
• 
  `Perpendicular = √(441 - 169)`
• 
  `Perpendicular = √(272)`
• 
  `Perpendicular = 16.5`

Therefore ,the measure of the third side would be equal to 16.5.

Answer 2

another side of the triangle is 16.5 approximately.

Explanation:

In a right angled triangle, the hypotenuse is the longest side and is opposite the right angle.

The perpendicular is the side that is perpendicular to the hypotenuse, and the base is the side that is adjacent to the perpendicular.

If the perpendicular and the hypotenuse are given, then the base can be found using the Pythagorean theorem.

The Pythagorean theorem states that in a right-angled triangle, the square of the hypotenuse is equal to the sum of the squares of the other two sides.

Note: Base and Perpendicular are determined by the taken angle

So, if the perpendicular is p and the hypotenuse is h, then the base can be found using the following formula:

`\boxed{\sf h^2 = p^2+b^2}`

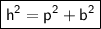
In this case:

The perpendicular is 13 and the hypotenuse is 21, then the base can be found using the following formula:

Given:

• hypotenuse(h )= 21

• perpendicular(p)= 13

To find

• base(b) =?

Solution:

We can use above formula or Pythagorean theorem:

Substituting value:

`\sf 21^2= 13^2+b^2`

`\sf b^2 = 21^2 -13^2`

`\sf b^2=272`

`\sf b= √(272)`

`\sf b \approx 16.5`

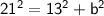
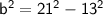
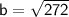
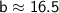
Therefore, another side of the triangle is 16.5