Question

In a recent poll a random sample of adults in some country (18 years and older) was asked, "When you see an ad emphasizing that a product is "Made in our country," are you more likely to buy it less likely to buy it, or neither more nor less likely to buy it?" The results of the survey, by age group, are presented in the following contingency table. Complete parts (a) through (c). What is the probability that a randomly selected individual is 35 to 44 years of age, given the individual is less likely to buy a product emphasized as "Made in our country"? The probability is approximately . (Round to three decimal places as needed.) What is the probability that a randomly selected individual is less likely to buy a product emphasized as "Made in our country," given the individual is 35 to 44 years of age? The probability is approximately . (Round to three decimal places as needed.) Are 18- to 34-year-olds more likely to buy a product emphasized as "Made in our country" than individuals in general?

Answer 1

a) The probability that a randomly selected individual is 35 to 44 years of age, given the individual is less likely to buy a product emphasized as "Made in our country is 0.036.

b) The probability that a randomly selected individual is less likely to buy a product emphasized as "Made in our country," given the individual is 35 to 44 years of age is 0.017.

c) Since 240 < 310 and 0.436 < 0.567, individuals aged 18–34 are not more likely than not to purchase products labeled as “Made in our Country.”

a) The probability that a randomly selected individual is less likely to buy a product emphasized as ‘Made in our Country’ can be calculated by dividing the number of individuals who are less likely to buy the product by the total number of individuals:

`P(\text{Less Likely}) = \frac{\text{Total Less Likely}}{\text{Total Individuals}} = (83)/(2296) \approx 0.036`

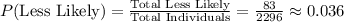
b) The probability that an individual is less likely to buy the product given they are aged 35 to 44 can be calculated by dividing the number of individuals aged 35 to 44 who are less likely to buy the product by the total number of individuals aged 35 to 44:

`P(\textLess Likely ) = \frac{\text{Less Likely and Age 35-44}}{\text{Total Age 35-44}} = (10)/(604) \approx 0.017`

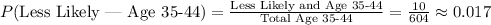
c) To determine if individuals aged 18–34 are more likely than not to purchase products labeled as “Made in our Country,” we can compare the number of individuals aged 18-34 who are more likely to buy the product with the number of individuals aged 18-34 who are less likely or neither more nor less likely to buy the product as follows:

The number of individuals Aged 18-34 more likely to buy = 240

The number of individuals Aged 18-34 less likely or neither more nor less likely = 310 (26 + 284)

The total number of individuals Aged 18-34 = 550

The proportion of individuals Aged 18-3 more likely to buy = 0.436 (240/550)

The proportion of individuals Aged 18-34 less likely or neither more nor less likely = 0.567 (310/550)

Question Completion:

Contingency Table

18 - 34 35 - 44 45 - 54 55 + Total

More Likely 240 384 391 405 1,420

Less Likely 26 10 29 18 83

Neither More Likely or Less Likely 284 210 164 135 793

Total 550 604 584 558 2,296