Question

The total surface area and slant height of a cone are 374 sq. cm and 10 cm respectively. Find the radius of the cone.​

Answer 1

`\mathrm{Solution:}\\\mathrm{Given:}\\\mathrm{Total\ surface\ area\ (TSA)=374cm^2}\\\mathrm{Slant\ height}(l)=\mathrm{10cm}\\\mathrm{Radius}(r)=?\\\mathrm{Now,}\\\mathrm{TSA\ of\ cone}=\pi r(r+l)\\\mathrm{or,\ }374=\pi r(r+10)\\\mathrm{or,\ }374=\pi r^2+10\pi r\\\mathrm{or,\ }(\pi)r^2+(10\pi)r-374=0`

`\therefore\ r=(-10\pi\pm√((10\pi)^2-4(\pi)(-374)))/(2\pi)=(-10\pi\pm75.41)/(2\pi)\\\mathrm{Taking\ only\ positive\ sign\ since\ radius\ cannot\ be\ negative,}\\\\r=(-10\pi+75.41)/(2\pi)=(312282)/(44599)\approx 7\mathrm{cm}`

Answer 2

7.00cm (3sf)

Explanation:

The total surface area of a cone is given by πr² + πrl, where r is the radius and l is the slant height. We can use the info in the question to form an equation as follows:

`\pi r^(2) + 10\pi r = 374`

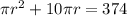
We can see that this is a quadratic equation in terms of r, so to solve it we bring all terms to one side and use the quadratic formula

`\pi r^(2) + 10\pi r - 374 = 0\\\\ r = \frac{-10\pi \pm \sqrt{(10\pi)^(2) - 4(\pi)(-374)}}{2\pi}`

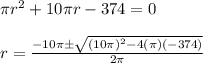
Plugging this into a calculator we get 2 solutions: r = -17.00 or r = 7.00

However as this is a length we only want positive solutions so we discard the negative root.