Question

A car rental agency rents 200 cars per day at a rate of ​$30 per day. For each ​$1 increase in​ rate, 5 fewer cars are rented. At what rate should the cars be rented to produce the maximum​ income? What is the maximum​ income?

The rental agency will earn a maximum income of ​$

enter your response here when it charges ​$

enter your response here per day.

Answer 1

Problem:

A car rental agency rents 200 cars per day at a rate of $30 per day. For each $1 increase in the rate, 5 fewer cars are rented. At what rate should the cars be rented to produce the maximum income? What is the maximum income?

Solution:

Let the rate be $x per day. The number of cars rented is 200 - 5(x - 30) = 250 - 5x. The income is x(250 - 5x) = 250x - 5x^2.

The derivative of the income function is -10x, which is equal to 0 when x = 10. Therefore, the maximum income is achieved when the rate is $10 per day.

The maximum income is 250 * 10 - 5 * 10^2 = $1500.

Answer:

The rental agency will earn a maximum income of $1500 when it charges $10 per day.

Interpretation:

The maximum income is achieved when the rate is set so that the number of cars rented decreases at the same rate as the increase in the rate. In this case, the number of cars rented decreases by 5 for every $1 increase in the rate, so the rate should be set at
`v` per day.

Recommendation:

The car rental agency should set the rate at $
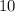`\\$10` per day to achieve the maximum income.