well, from the graph above, we can say that the polynomial has "zeros" at -6 , 4 , 5, and we also know that it passes through (0 , 60).
Let's reword that and say instead, what's the function whose roots are -6, 4 and 5 and it passes through (0 , 60)?
![\begin{cases} x = -6 &\implies x +6=0\\ x = 4 &\implies x -4=0\\ x = 5 &\implies x -5=0\\ \end{cases} \\\\[-0.35em] ~\dotfill\\\\ \stackrel{original~polynomial}{a ( x +6 )( x -4 )( x -5 ) = \stackrel{0}{y}} \hspace{5em}\textit{we also know that } \begin{cases} x=0\\ y=60 \end{cases} \\\\\\ a ( 0 +6 )( 0 -4 )( 0 -5 ) = 60\implies 120a=60\implies a=\cfrac{60}{120}\implies a=\cfrac{1}{2} \\\\[-0.35em] ~\dotfill](https://img.qammunity.org/2024/formulas/mathematics/college/kl2e8ilzr3fe9ondfiwomhdlujpyvdrvg5.png)
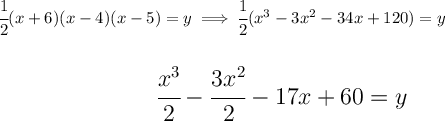
Check the picture below.