Question

NO LINKS!!! URGENT HELP PLEASE!!

1. Find a complete factorization of x^4 - 4x^3 + 4x^2 - 36x - 45, given that 5 and -1 are roots.


a. (x + 5)(x - 1)( x - 3i)(x + 3i)

b. (x - 5)(x + 1)(x^2 - 9)

c. (x - 5)(x + 1)(x + 9)

d. (x - 5)(x + 1)(x - 3i)(x + 3i)


2. Find a factorization of 3x^3 - 27x^2 + 93x - 165, given that 5 and 2 + i√(7) are roots.

a. 3(x - 5)(x^2 - 4x + 11)

b. (x - 5)(x^2 - 4x + 11)

c. 3(x + 5)(x^2 + 4x - 7)

d. 3(x + 5)(x^2 - 4x + 7)

Answer 1

`\textsf{1)}\quad \textsf{d.}\;\;(x - 5)(x + 1)(x - 3i)(x + 3i)`

`\textsf{2)}\quad \textsf{a.}\;\;3(x - 5)(x^2 - 4x + 11)`

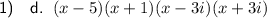
Explanation:

Question 1

To find a factorization of the polynomial x⁴ - 4x³ + 4x² - 36x - 45, we can start by using the given roots to determine some of the factors.

Given roots:

• 5
• -1

To find the factors corresponding to the roots -5 and -1 we can use the factor theorem that states that if a polynomial f(x) has a root r, then (x - r) is a factor of f(x).

Therefore, two factors of the given polynomial are:

• 
  `(x - 5)`

• 
  `(x - (-1)) = (x + 1)`

Multiply the two linear factors:

`\begin{aligned}(x-5)(x+1)&=x^2+x-5x-5\\&=x^2-4x-5\end{aligned}`

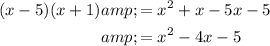
As the polynomial we wish to factor is quartic, and the multiplied factors return a quadratic polynomial, the remaining factor must be quadratic.

Perform long division to find the remaining linear factor:

`\large \begin{array}{r}x^2+9\phantom{)}\\x^2-4x-5{\overline{\smash{\big)}\,x^4 - 4x^3 + 4x^2 - 36x - 45\phantom{)}}}\\{-~\phantom{(}\underline{(x^4-4x^3-5x^2)\phantom{-..............)}}\\9x^2-36x-45\phantom{)}\\-~\phantom{()}\underline{(9x^2-36x-45)\phantom{}}\\0\phantom{)}\\\end{array}`

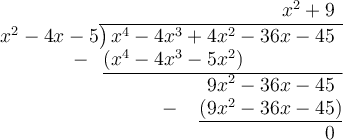
Therefore, the three factors are:

• (x - 5)
• (x + 1)
• (x² + 9)

We can factor x² + 9 further.

As the discriminant of x² + 9 = 0 is less than zero, it indicates it has complex roots. Substituting a = 1, b = 0 and c = 9 into the quadratic formula, we get:

`x=(-0\pm√(0^2-4(1)(9)))/(2(1))`

`x=(\pm√(-36))/(2)`

`x=(\pm√(6^2 \cdot (-1)))/(2)`

`x=(\pm√(6^2 )√((-1)))/(2)`

`x=(\pm6\:i)/(2)`

`x=\pm3\:i`

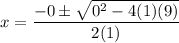
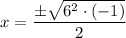
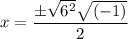
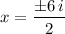
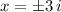
Therefore, x² + 9 factored is (x - 3i)(x + 3i).

So, the fully factored polynomial is:

`\large\boxed{\boxed{(x-5)(x+1)(x-3i)(x+3i)}}`

`\hrulefill`

Question 2

To find a factorization of the polynomial x³ - 27x² + 93x - 165, we can start by using the given roots to determine some of the factors.

Given roots:

• 5
• 
  `2 + i√(7)`

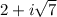
Since complex roots occur in conjugate pairs for polynomials with real coefficients, we also have the root
`(2 - i√(7))`.

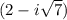The factor theorem states that if a polynomial f(x) has a root r, then (x - r) is a factor of f(x). Therefore, three factors of the given polynomial are:

• 
  `(x -5)`

• 
  `(x-(2 + i√(7)))=(x-2-i√(7))`

• 
  `(x-(2 - i√(7)))=(x-2+i√(7))`

Multiply the two complex factors:

`\begin{aligned}(x-2-i√(7))(x-2+i√(7))&=x^2-2x+i√(7)x-2x+4-2i√(7)-i√(7)x+2i√(7)-7i^2\\&=x^2-4x+4-7(-1)\\&=x^2-4x+11\end{aligned}`

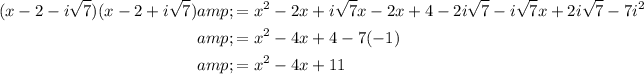
Multiply the product of the two complex factors by the linear factor (x - 5):

`\begin{aligned}(x^2-4x+11)(x-5)&=x^3-5x^2-4x^2+20x+11x-55\\&=x^3-9x^2+31x-55\end{aligned}`

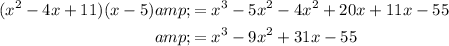
If we compare the product of the three factors with the given polynomial, we can see that the given polynomial is three times the product of the factors. Therefore, the leading coefficient is 3.

So, the fully factored polynomial is:

`\large\boxed{\boxed{3(x-5)(x^2-4x+11)}}`