Question

Find the angle between the vectors.
u= (6,2)
v = (7,0)

Answer 1

Hi,

18.4349488... °

Explanation:

`\\||\overrightarrow{u}||=√(6^2+2^2) =√(40) \\||\overrightarrow{v}||=√(7^2+0^2) =7\\\overrightarrow{u}.\overrightarrow{v}=(6,2)*\left(\begin{array}{c}7\\ 0\end{array}\right)=42=||\overrightarrow{u}||*||\overrightarrow{v}||*cos(\alpha)\\cos(\alpha)=(42)/(7*√(40) ) =0.94868329...\\\alpha=18.4349488..^o\\`

Answer 2

18.43°

Explanation:

The angle between two vectors can be found using the following formula:

`\boxedv`

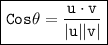
where:

• θ is the angle between the vectors
• u ⋅ v is the dot product of the vectors
• |u| is the magnitude of vector u
• |v| is the magnitude of vector v

For the vectors u = (6, 2) and v = (7, 0), we have:

`\tt u \cdot v = 6 * 7 + 2 * 0 = 42`

`\tt |u| = √(6^2 + 2^2)= 2√(10)`

`\tt |v| = √(7^2 + 0^2) = 7`

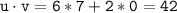
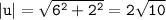
Now, substituting the value

`\tt Cos \theta =(42)/(2√(10)*7)`

`\tt Cos \theta =(3)/(√(10))`

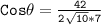
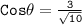
solving for
`\theta`

we get

`\tt \theta=cos^(-1)((3)/(√(10)))`

`\tt \theta=18.43 ^0`

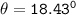
Therefore, the angle between the vectors u = (6, 2) and v = (7, 0) is 18.43°.