Question

Light with a wavelength of 605.0 nm looks orange. What is the energy, in joules, per photon of this orange light?

___J?
What is the energy in eV? (1 eV = 1.60217653 ✕ 10−19 J)
____eV?
please help fast i need this within an hour

Answer 1

Approximately
`3.283 * 10^(-19)\; {\rm J}`;

Approximately
`2.049 \; {\rm eV}`.

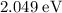(Assumption: the wavelength was measured in vacuum, where the speed of light is
`c \approx 2.9979* 10^(8)\; {\rm m\cdot s^(-1)}`.)

Step-by-step explanation:

The per-photon energy of this light can be found from its wavelength through the following steps:

• Find the frequency of this light from its wavelength.
• Find the per-photon energy of this light using the Planck Energy-Frequency Relation.

It is given that the wavelength of this light is
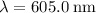`\lambda = 605.0\; {\rm nm}`. In standard units (meters,) the wavelength of this light would be:

`\begin{aligned}\lambda &= 605.0\; {\rm nm}* \frac{1\; {\rm m}}{10^(9)\; {\rm nm}} \\ &= 6.050 * 10^(-7)\; {\rm m}\end{aligned}`.

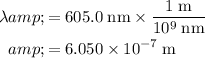To find the frequency
`f` of this light, divide the wave speed
`c \approx 2.9979* 10^(8)\; {\rm m\cdot s^(-1)}` by the wavelength:

`\begin{aligned}f &= (c)/(\lambda) \\ &\approx \frac{2.9979* 10^(8)\; {\rm m\cdot s^(-1)}}{6.050 * 10^(-7)\; {\rm m}} \\ &\approx 4.9552 * 10^(14)\; {\rm s^(-1)}\end{aligned}`.

By the Planck Energy-Frequency Relation, if the frequency of an electromagnetic wave is
`f`, the per-photon energy
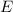`E` of this wave would be:

`\displaystyle E = h\, f`,

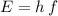Where
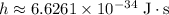`h \approx 6.6261* 10^(-34)\; {\rm J\cdot s}` is the Planck Constant.

Substitute in
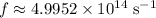`f \approx 4.9952 * 10^(14)\; {\rm s^(-1)}` and evaluate to find the per-photon energy of this wave:

`\begin{aligned}E &= h\, f \\ &\approx (6.6261 * 10^(-34)\; {\rm J\cdot s^(-1)})\, (4.9952 * 10^(14)\; {\rm s^(-1)}) \\ &\approx 3.2833 * 10^(-19)\; {\rm J}\end{aligned}`.

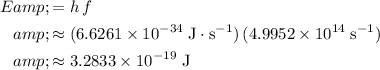Given that
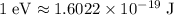`1\; {\rm eV} \approx 1.6022 * 10^(-19)\; {\rm J}`, this per-photon energy would be equivalent to:

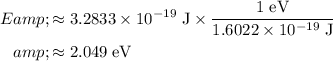`\begin{aligned}E &\approx 3.2833 * 10^(-19)\; {\rm J} * \frac{1\; {\rm eV}}{1.6022 * 10^(-19)\; {\rm J}} \\ &\approx 2.049\; {\rm eV}\end{aligned}`.