Question

(3x−2) (x+3) (2x+1) = 0 How Many distinct roots does this equation have???

Answer 1

This equation have 3 distinct roots

Step-by-step explanation:

Distinct Roots are unique roots/ solutions that make the equation equal to zero.

In order to find the roots of an equation you have to first set each factor equal to zero, then solve for x.

1.
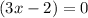
`(3x-2)=0`

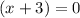
`3x=2`

`x=2/3`

2.
`(x+3)=0`

`x=-3`

3.
`(2x+1)=0`

`2x=-1`

`x=-1/2`

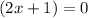
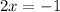
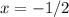
The equation have 3 unique solutions: x= 2/3, -3, and -1/2

Answer 2

The equation (3x−2) (x+3) (2x+1) = 0 has 3 distinct roots.

Step-by-step explanation:

The roots of the equation are the values of x that make the equation equal to 0. We can find the roots by setting each factor equal to 0 and solving the resulting equations.

(3x−2) (x+3) (2x+1) = 0

solving for x.

either

3x-2=0

3x=2

`\tt x=(2)/(3)`

or,

(x+3)=0

x=-3

or

2x+1=0

`\tt x=-(1)/(2)`

Therefore, the roots of the equation are:
`\boxed{\tt x=(2)/(3),-3,-(1)/(2).}` These are all distinct roots, so the equation has 3 distinct roots.