Total Electric Field in Air is
![\[ E = Z_0 H \]](https://img.qammunity.org/2024/formulas/physics/high-school/enz0meyjo8mpyvgbj0ixox651de8gifhud.png) .where H is the magnetic field amplitude of the incident wave and Z0 is the impedance of free space.
.where H is the magnetic field amplitude of the incident wave and Z0 is the impedance of free space.
Given a uniform plane wave in air with
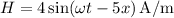 , the electric field in air
, the electric field in air
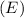 is related to the magnetic field (\( H \)) by the impedance of free space
is related to the magnetic field (\( H \)) by the impedance of free space
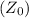 :
:
![\[ E = Z_0 H \]](https://img.qammunity.org/2024/formulas/physics/high-school/enz0meyjo8mpyvgbj0ixox651de8gifhud.png)
The impedance of free space
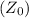 is given by:
is given by:
![\[ Z_0 = \sqrt{(\mu_0)/(\varepsilon_0)} \]](https://img.qammunity.org/2024/formulas/physics/high-school/himar1ua89ja4bx1f1tflx4589ni6jlhsp.png)
where
 is the permeability of free space, and
is the permeability of free space, and
 is the permittivity of free space.
is the permittivity of free space.
(a) Total Electric Field in Air:
![\[ E = Z_0 H \]](https://img.qammunity.org/2024/formulas/physics/high-school/enz0meyjo8mpyvgbj0ixox651de8gifhud.png)
(b) Time-Average Power Density in the Plastic Region:
The time-average power density
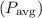 in the plastic region is given by:
in the plastic region is given by:
![\[ P_{\text{avg}} = (1)/(2) \text{Re} \left\{ E * H^* \right\} \]](https://img.qammunity.org/2024/formulas/physics/high-school/cll8077bdqv7esj76x8n63qt9nsbw3ar4v.png)
where
 is the complex conjugate of
is the complex conjugate of
 .
.
(c) Standing Wave Ratio (SWR):
The standing wave ratio (SWR) is given by:
![\[ \text{SWR} = \frac{E_{\text{max}}}{E_{\text{min}}} \]](https://img.qammunity.org/2024/formulas/physics/high-school/ab0ir04kveqijeanq9wc76ityyqb8cs65e.png)
where
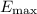 is the maximum amplitude of the electric field, and
is the maximum amplitude of the electric field, and
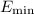 is the minimum amplitude of the electric field.
is the minimum amplitude of the electric field.
Let's calculate each of these:
(a) Total Electric Field in Air:
![\[ E = Z_0 H \]](https://img.qammunity.org/2024/formulas/physics/high-school/enz0meyjo8mpyvgbj0ixox651de8gifhud.png)
(b) Time-Average Power Density in the Plastic Region:
![\[ P_{\text{avg}} = (1)/(2) \text{Re} \left\{ E * H^* \right\} \]](https://img.qammunity.org/2024/formulas/physics/high-school/cll8077bdqv7esj76x8n63qt9nsbw3ar4v.png)
(c) Standing Wave Ratio (SWR):
![\[ \text{SWR} = \frac{E_{\text{max}}}{E_{\text{min}}} \]](https://img.qammunity.org/2024/formulas/physics/high-school/ab0ir04kveqijeanq9wc76ityyqb8cs65e.png)
If you have specific values for
 ,
,
 , and
, and
 , please provide them so that we can proceed with the calculations.
, please provide them so that we can proceed with the calculations.