The expected value of the sampling distribution of the sample mean is approximately -9.1, and the standard error is approximately 0.2885.
The expected value (mean) of the sampling distribution of the sample mean (often denoted as
 ) is equal to the population mean (μ). The standard error of the sample mean (
) is equal to the population mean (μ). The standard error of the sample mean (
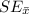 ) is calculated using the formula:
) is calculated using the formula:
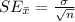
where:
 is the population standard deviation,
is the population standard deviation,
n is the sample size.
Given that μ=−9.1, σ=2, and n=48, we can calculate the expected value and the standard error:
Expected Value
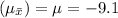
Standard Error

Let's calculate the values:
Expected Value
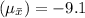
Standard Error
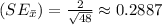
Rounded to the specified decimal places:
Expected Value
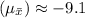
Standard Error
