Question

The common ratio in a geometric sequence is 4 and the first term is 3 find the sum of the first 8 terms in the sequence

Answer 1

65 535

Explanation:

`S_(n) =(ar^(n)-1)/(r-1)`

r=common ratio,a=first term,n=no. of terms

`(3 * (4^8 - 1))/((4 - 1))`

`(3 * (65,536 - 1) )/(3)`

`( 3 * 65,535 )/(3)`

S=65 535

Answer 2

65535

Explanation:

To find the sum of the first 8 terms of a geometric sequence, we can use the formula for the sum of a geometric series:

`S_n=(a(1-r^n))/(1-r)`

where:

• Sₙ is the sum of the series.
• a is the first term of the series
• r is the common ratio.
• n is the number of terms.

Given values:

• a = 3
• r = 4
• n = 8

Substitute the given values into the formula and solve for S₈:

`S_8=(3(1-4^8))/(1-4)`

`S_8=(3(1-65536))/(1-4)`

`S_8=(3(-65535))/(-3)`

`S_8=65535`

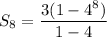
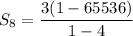
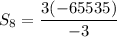
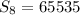
Therefore, the sum of the first 8 terms in the given geometric sequence is 65535.