The bone discovered which has 10 percent of the carbon-14 found in the bones of other living animals is 19154 years old.
The process of carbon-14 decay can be modeled using the exponential decay formula:
![\[ N(t) = N_0 \cdot e^(-rt) \]](https://img.qammunity.org/2024/formulas/biology/high-school/58i8vhuedci9kz33o011v5lgatdjc8w58q.png)
Where:
 is the amount of substance at time
is the amount of substance at time
 .
.
 is the initial amount of substance.
is the initial amount of substance.
 is the decay rate constant.
is the decay rate constant.
 is time.
is time.
Given that the half-life of carbon-14 is 5730 years, we can determine the decay rate constant
 using the formula for exponential decay:
using the formula for exponential decay:
![\[ \text{Half-life} = (\ln(2))/(r) \ \\\\[ r = \frac{\ln(2)}{\text{Half-life}} \ \\\\[ r = (\ln(2))/(5730) \ \\\\[ r \approx 0.00012097 \text{ per year} \]]()
Now, we're given that the bone has 10% of the carbon-14 found in living animals. This means the remaining amount after decay is 10% of the initial amount
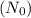 .
.
Let
 be the time passed.
be the time passed.
![\[ N(t) = 0.1 \cdot N_0 = N_0 \cdot e^(-rt) \]](https://img.qammunity.org/2024/formulas/biology/high-school/kyyqyzh35tr36r3r71gs4zax5fez99ypr3.png)
Since we know the relationship between the remaining amount and the initial amount, we can set up an equation to solve for
 :
:
![\[ 0.1 \cdot N_0 = N_0 \cdot e^(-rt) \ \\\\[ e^(-rt) = 0.1 \ \\\\[ -rt = \ln(0.1) \ \\\\[ t = -(\ln(0.1))/(r) \ \\\\[ t = -(\ln(0.1))/(0.00012097) \ \\\\[ t \approx 19154 \text{ years} \]]()
Therefore, the bone is approximately 19154 years old.