Question

would teh slope of the regression line change if the point (26, 601) were removed from the data set? in what direction?

Answer 1

Removing a significant outlier from a data set can affect the slope of the regression line and typically results in a stronger correlation, indicated by an r-value closer to 1. The slope may increase or decrease depending on the position of the outlier.

Step-by-step explanation:

When assessing whether the slope of a regression line would change if a specific point were removed, one must consider how influential that point is on the regression analysis. If the point is a significant outlier, it could have a noticeable effect on both the slope and correlation coefficient, r-value.

Removing an influential point often results in a regression line that better fits the remaining data set, typically characterized by a higher r-value closer to 1 (which indicates a stronger linear relationship) and a changed slope. The direction in which the slope would change depends on the position of the outlier relative to the current line of best fit. If the outlier is above or below the regression line and away from the center of the data distribution, the line's slope may increase or decrease once the point is removed.

Answer 2

Removing the point (26, 601) from the data set would likely change the slope of the regression line, and the direction of the change is difficult to predict without further information.

Influence of outliers: The point (26, 601) appears to be an outlier, meaning it lies far away from the general trend of the data. Removing an outlier can significantly affect the calculations used to find the least-squares line, including the slope.

Direction of change: Predicting the specific direction of change (increase or decrease) is challenging without knowing the distribution of the remaining data points. If the removed point was pulling the line upwards, removing it could result in a flatter slope or even a slight decrease. Conversely, if the point was suppressing the line, its removal could cause the slope to become steeper.

Therefore, while we can confidently say that removing the outlier would impact the slope, determining the direction of change requires more information about the remaining data points.

Complete Question:
The equation of the least-squares regression line is
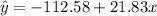`$\hat{y}=-112.58+21.83 x$`, where
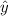`$\hat{y}$` is the predicted number of property crimes and x is the student enrollment in thousands.
Would the slope of the regression line change if the points (26, 601) were removed from the data set? If so, in what direction?