Question

Bicycles arrive at a bike shop in boxes. Before they can be​ sold, they must be​ unpacked, assembled, and tuned​ (lubricated, adjusted,​ etc.). Based on past​ experience, the shop manager creates a model of how long this may take based on the assumptions that the times for each setup phase are​ independent, each phase follows a Normal​ model, and the means and standard deviations of the times in minutes are as shown in the table. Complete parts​ a) and​ b).

Phase

Mean

SD

Unpacking

3.3

0.8

Assembly

23.9

2.7

Tuning

12.7

2.8

Question content area bottom Part 1

​a) What are the mean and the standard deviation for the total bicycle setup​ time? μ=enter your response here σ=enter your response here ​(Round to two decimal places as​ needed.)

Answer 1

The mean total bicycle setup time is 39.9 minutes, and the standard deviation is approximately 3.97 minutes.

Step-by-step explanation:

To calculate the mean for the total bicycle setup time, we add up the means for each phase: unpacking, assembly, and tuning. Therefore, the mean total time (μ) would be 3.3 minutes + 23.9 minutes + 12.7 minutes, which equals 39.9 minutes.

Next, to calculate the standard deviation (σ) for the total bicycle setup time, we use the property that the variance of independent variables adds up. Since standard deviation is the square root of variance, we first square the individual standard deviations, add them up, and finally take the square root of the sum. So, the calculation would be

σ
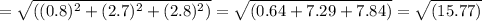`= √(((0.8)^2 + (2.7)^2 + (2.8)^2)) = √((0.64 + 7.29 + 7.84)) = \sqrt{(15.77)`, which equals approximately 3.97 minutes.