Answer:
The lines are:
Explanation:
The given equation is:
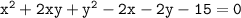
We can write this equation in the standard form of a quadratic equation as follows:
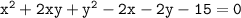
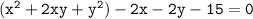
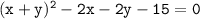
Using formula of
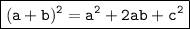
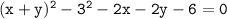
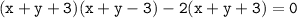
using formula of
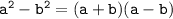
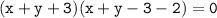
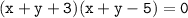
This equation tells us that the two lines represented by the equation are:
Solving the first equation for x, we get:
x=-y+5
So, the first line has an intercept of (0, 5) and a slope of -1.
Solving the second equation for x, we get:
x=-y-3
So, the second line has an intercept of (0, -3) and a slope of -1.
Therefore, the two lines represented by the equation
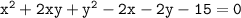 are:
are: