Answer:
Approximately
 (approximately
(approximately
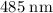 .)
.)
Step-by-step explanation:
The wavelength of this photon can be found in the following steps:
- Find the momentum of the given electron.
- Apply the relationship between the wavelength and momentum of a photon to find the required wavelength.
Since the electron in this question is travelling at a relatively low velocity of
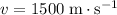 , the momentum
, the momentum
 of this electron can be approximated as:
of this electron can be approximated as:
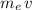 ,
,
Where
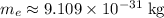 is the electron rest mass (mass of an electron that isn't moving.)
is the electron rest mass (mass of an electron that isn't moving.)
Substitute in
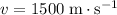 to obtain:
to obtain:
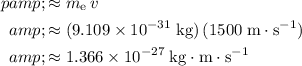 .
.
The momentum
 of a photon is inversely proportional to its wavelength
of a photon is inversely proportional to its wavelength
 :
:
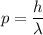 ,
,
Where
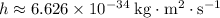 is the Planck constant.
is the Planck constant.
Rearrange this equation to find wavelength
 in terms of momentum
in terms of momentum
 :
:
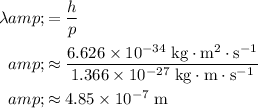 .
.