Question

Given the side lengths of 4, 5, and 6, the triangle is:

acute.
obtuse.
right.
None of these choices are correct.

Answer 1

Acute

Explanation:

It is not a right triangle. Because the biggest angle is less than , the other two angles are also, and the triangle is an (a) Acute triangle.

Answer 2

Answer: Acute

Explanation

Refer to the converse of the pythagorean theorem. That theorem converse has three cases.

• If
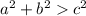  `a^2+b^2 > c^2` then the triangle is acute.
• If
  `a^2+b^2 = c^2` then it is a right triangle.
• If
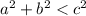  `a^2+b^2 < c^2` then the triangle is obtuse.

The a,b,c refer to the side lengths. The c is the longest side.

In this case

a = 4, b = 5, c = 6

We find that
`a^2+b^2 = 4^2+5^2 = 16+25 = 41`

And also
`c^2 = 6^2 = 36`

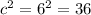
Compare
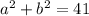`a^2+b^2 = 41` and
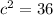`c^2 = 36` to see that 41 is larger, so we'll go with the case
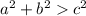`a^2+b^2 > c^2` to prove the triangle is acute.

You can use a tool like GeoGebra to confirm the answer is correct.