Question

Given the side lengths of 2, 2, and 3, the triangle is:

acute.
obtuse.
right.
None of these choices are correct.

Answer 1

Answer: Obtuse

Step-by-step explanation:

The converse of the pythagorean theorem has 3 cases

• If
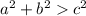  `a^2+b^2 > c^2` then the triangle is acute.
• If
  `a^2+b^2 = c^2` then we have a right triangle.
• If
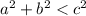  `a^2+b^2 < c^2` then the triangle is obtuse.

a = 2, b = 2, c = 3 are the three sides. C is always the largest side.

`a^2+b^2 = 2^2+2^2 = 8`

`c^2 = 3^2 = 9`

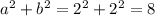
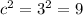
We can see that
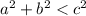`a^2+b^2 < c^2` (since 8 < 9), which leads to the triangle being obtuse. The obtuse angle is opposite the longest side.

You can use a tool like GeoGebra to confirm the answer.