Question

Find y' by (a) applying the Product Rule and (b) multiplying the factors to produce a sum of simpler terms to differentiate.

Answer 1

`y'=-5x^4+33x^2-6x-28`

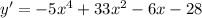
Explanation:

Differentiate the following function using the product rule.

`y=(7-x^2)(x^3-4x+3)\\\\\\\hrule`

I will be using the following rules of differentiation:

`\boxed{\left\begin{array}{ccc}\text{\underline{The Product Rule:}}\\(d)/(dx)[f(x)g(x)]= f(x)g'(x)+g(x)f'(x)\end{array}\right } \\ \\\\ \boxed{\left\begin{array}{ccc}\text{\underline{The Power Rule:}}\\(d)/(dx)[x^n]= nx^(n-1)\end{array}\right } \\\\\\ \boxed{\left\begin{array}{ccc}\text{\underline{The Constant Rule:}}\\(d)/(dx)[a]= 0\end{array}\right }`
`\hrulefill`

(a) Applying the product rule as is:

`y'=(7-x^2)(d)/(dx) [x^3-4x+3]+(x^3-4x+3)(d)/(dx)[7-x^2]\\\\\\\\ \Longrightarrow y'=(7-x^2)(3x^2-4)+(x^3-4x+3)(-2x)\\\\\\\\\Longrightarrow y'=-3x^4+25x^2-28-2x^4+8x^2-6x\\\\\\\\\therefore \boxed{\boxed{y'=-5x^4+33x^2-6x-28}}`

(b) Multiplying the factors to produce a sum of simpler terms:

`y=(7-x^2)(x^3-4x+3)\\\\\\\\\Longrightarrow y=-x^5+11x^3-3x^2-28x+21`

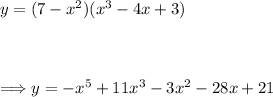
Now differentiating, notice we can just apply the power rule to each term

`y'=(d)/(dx)[ -x^5+11x^3-3x^2-28x+21]\\\\\\\\\therefore \boxed{\boxed{y'=-5x^4+33x^2-6x-28}}`

Notice how we get the same answer using different methods. As you get more familiar with derivatives you'll soon be able to recognize easier methods to derive functions.