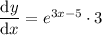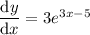From first principle,find the derivative of \tt {e}^(3x - 5) Help!!​

Question

From first principle,find the derivative of
`\tt {e}^(3x - 5)`
Help!!​

Answer 1

`\frac{\text{d}y}{\text{d}x}=3e^(3x-5)`

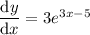
Explanation:

Differentiating from First Principles is a technique to find an algebraic expression for the gradient at a particular point on the curve.

`\boxed{\begin{minipage}{5.6 cm}\underline{Differentiating from First Principles}\\\\\\$\text{f}\:'(x)=\displaystyle \lim_(h \to 0) \left[\frac{\text{f}(x+h)-\text{f}(x)}{(x+h)-x}\right]$\\\\\end{minipage}}`

The point (x + h, f(x + h)) is a small distance along the curve from (x, f(x)).

As h gets smaller, the distance between the two points gets smaller.

The closer the points, the closer the line joining them will be to the tangent line.

To differentiate y = e^(3x-5) using first principles, substitute f(x + h) and f(x) into the formula:

`\displaystyle \frac{\text{d}y}{\text{d}x}=\lim_(h \to 0) \left[(e^(3(x+h)-5)-e^(3x-5))/((x+h)-x)\right]`

Simplify the numerator:

`\displaystyle \frac{\text{d}y}{\text{d}x}=\lim_(h \to 0) \left[(e^(3x+3h-5)-e^(3x-5))/((x+h)-x)\right]`

`\displaystyle \frac{\text{d}y}{\text{d}x}=\lim_(h \to 0) \left[(e^(3x-5)e^(3h)-e^(3x-5))/(h)\right]`

`\displaystyle \frac{\text{d}y}{\text{d}x}=\lim_(h \to 0) \left[(e^(3x-5)(e^(3h)-1))/(h)\right]`

Apply the Product Law for Limits, which states that the limit of a product of functions equals the product of the limit of each function:

`\displaystyle \frac{\text{d}y}{\text{d}x}=\lim_(h \to 0)\left[e^(3x-5)\right] \cdot \lim_(h \to 0) \left[((e^(3h)-1))/(h)\right]`

Since the first function does not contain h, it is not affected by the limit:

`\displaystyle \frac{\text{d}y}{\text{d}x}=e^(3x-5)\cdot \lim_(h \to 0) \left[((e^(3h)-1))/(h)\right]`

Transform the numerator of the second function.

`\textsf{Let\;\;$e^(3h)-1=n \implies e^(3h)=n+1$}`

`\textsf{You will notice that as\;\;$h \to 0, \;e^(3h) \to 1$,\;so\;\;$n \to 0$.}`

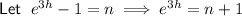
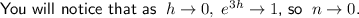
Take the natural log of both sides and rearrange to isolate h:

`\ln e^(3h)=\ln(n+1)`

`3h=\ln(n+1)`

`h=(1)/(3)\ln(n+1)`

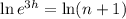
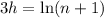
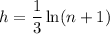
Therefore:

`\displaystyle \frac{\text{d}y}{\text{d}x}=e^(3x-5)\cdot \lim_(n \to 0) \left[(n)/((1)/(3)\ln(n+1))\right]`

`\displaystyle \frac{\text{d}y}{\text{d}x}=e^(3x-5)\cdot \lim_(n \to 0) \left[(3n)/(\ln(n+1))\right]`

Rewrite the fraction as 1 divided by the reciprocal of the fraction:

`\displaystyle \frac{\text{d}y}{\text{d}x}=e^(3x-5)\cdot \lim_(n \to 0) \left[(1)/((\ln(n+1))/(3n))\right]`

`\displaystyle \frac{\text{d}y}{\text{d}x}=e^(3x-5)\cdot \lim_(n \to 0) \left[(1)/((1)/(3n)\ln(n+1))\right]`

`\displaystyle \frac{\text{d}y}{\text{d}x}=e^(3x-5)\cdot \lim_(n \to 0) \left[(3)/((1)/(n)\ln(n+1))\right]`

Apply the Log Power Law:

`\displaystyle \frac{\text{d}y}{\text{d}x}=e^(3x-5)\cdot \lim_(n \to 0) \left[\frac{3}{\ln(n+1)^{(1)/(n)}}\right]`

Apply the Quotient Law for Limits, which states that the limit of a quotient of functions equals the quotient of the limit of each function:

`\frac{\text{d}y}{\text{d}x}=e^(3x-5)\cdot \left[\frac{\displaystyle\lim_(n \to 0)3}{\displaystyle\lim_(n \to 0)\ln(n+1)^{(1)/(n)}}\right]`

Therefore, the numerator is a constant:

`\frac{\text{d}y}{\text{d}x}=e^(3x-5)\cdot \left[\frac{3}{\displaystyle\lim_(n \to 0)\ln(n+1)^{(1)/(n)}}\right]`

The limit of a function is the function of the limit.

Move the limit inside and take the natural log of that limit:

`\frac{\text{d}y}{\text{d}x}=e^(3x-5)\cdot \left[\frac{3}{\displaystyle \ln\left(\lim_(n \to 0)(n+1)^{(1)/(n)}\right)}\right]`

The definition of e is:

`\boxed{e=\lim_(n \to 0)(n+1)^{(1)/(n)}}`

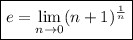
Therefore:

`\frac{\text{d}y}{\text{d}x}=e^(3x-5)\cdot \left[(3)/(\displaystyle \ln\left(e\right))\right]`

As ln(e) = 1, then:

`\frac{\text{d}y}{\text{d}x}=e^(3x-5)\cdot \left[(3)/(1)\right]`

`\frac{\text{d}y}{\text{d}x}=e^(3x-5)\cdot 3`

`\frac{\text{d}y}{\text{d}x}=3e^(3x-5)`