Question

how many terms are needed in series (3) to compute cos x for |x| < 1/2 accurate to 12 decimal places (rounded)?

Answer 1

Explanation:

We should use the Lagrange Error Bound equation, which states that

In calculus, the Taylor series expansion of a function is a representation of the function as an infinite sum of terms. The terms of the Taylor series are calculated based on the function's derivatives evaluated at a specific point. However, when using a Taylor polynomial of finite degree to approximate a function, there will always be some error between the true function and its approximation.

This error can be modeled as

`|R_n|\leq (f^((n+1)) (c) |x-a|^(n+1) )/((n+1)!) \\`

Where f(x) is the function

R_n is the LaGrange error

n is the number of terms

a is the center of the Taylor polynomial expression

c is some point that exist on the interval [a,x]

In the expression, the center of the polynomial is 0

So, what is the Taylor polynomial for cos?

Well, we know that

`cos(x)=1-(x^(2) )/(2!) +(x^4)/(4!) -(x^6)/(6!) +.........((-1)^n)/((2n)!) x^n\\`

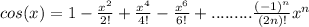
So, our f(x) is the Taylor polynomial of cosine

We also know that the max of cosine or sine is 1 ,

Finally, our error should be greater than or equal to 0.000000000001

So, R_n<=0.000000000001

`R_n\leq (|x|^(n+1) )/((n+1)!)`

Let x=1/2

`(0.5^(n+1) )/((n+1)!)\leq 0.000000000001`

Using trial and error, we get n=11.