Final Answer:
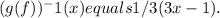
The composition
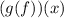 simplifies to
simplifies to
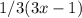 by substituting the given functions g(x) and f(x) and finding the inverse.
by substituting the given functions g(x) and f(x) and finding the inverse.
Step-by-step explanation:
The composition (g(f))(x) represents the combination of the functions g and f, denoted as g(f(x)). To find the inverse of this composition, we set the entire expression equal to x and solve for the variable. Let
 , then
, then
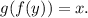
Given
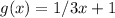 and
and
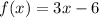 , we first find
, we first find
 . Substituting f(x) into g(x), we get
. Substituting f(x) into g(x), we get
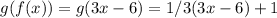 . Simplifying this expression yields
. Simplifying this expression yields
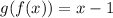 .
.
Now, we have y = x - 1. To find the inverse, we switch x and y and solve for y. Swap x and y: x = y - 1. Solving for y, we get y = x + 1.
However, the original question asked for (g(f))^-1(x), so we substitute this expression back into the result for
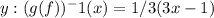 . Therefore, the final answer is
. Therefore, the final answer is
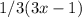 .
.