Question

5. Rosa joins a club to prepare to run a marathon. During the first training session Rosa runs a distance of 3000 metres. Each training session she increases the distance she runs by 400 metres.

a. Write down the distance Rosa runs in the third training session;
b. Write down the distance Rosa runs in the nth training session
c. A marathon is 42.195 kilometres. In the kth training session Rosa will run further than a marathon for the first time. Find the value of k.

Answer 1

Rosa runs 3800 m in the third session, and the distance for the nth session is given by the formula 3000 + (n - 1) * 400. To find the kth session where she exceeds the marathon distance, we solve the inequality 3000 + (k - 1) * 400 > 42195.

Step-by-step explanation:

To solve the problem regarding Rosa's marathon training:

1. Distance in the third training session: Rosa runs 3000 m in the first session and increases her distance by 400 m each time. To find the distance for the third training session, we add two increments of 400 m to the initial distance: 3000 m + 2(400 m) = 3000 m 800 m = 3800 m. Therefore, Rosa runs 3800 m in the third training session.
2. Distance in the nth training session: The distance Rosa runs in the nth training session can be represented by the arithmetic sequence d_n = 3000 + (n - 1) * 400, where d_n is the distance run in the nth session.
3. Value of k when Rosa runs further than a marathon: A marathon is 42.195 km, which is equal to 42195 m. To find the kth session where she first exceeds this distance, we use the arithmetic sequence formula to set up the inequality: 3000 + (k - 1) * 400 > 42195. Solving for k gives us the smallest whole number that satisfies the inequality.

Answer 2

a. 3800 m

b. 3000 + 400(n - 1)

c. k = 99

Step-by-step explanation:

The question tells us that Rosa runs 3000 metres in her first training session, and increases the distance by 400 metres each session thereafter.

a. To calculate the distance she runs in the third session, we have to add two 400-metres to the first session's 3000 metres, as she increased her distance twice since the first session. Therefore:

distance = 3000 + (2 × 400)

= 3000 + 800

= 3800 m

b. From the previous question, we can see that for the nth session, we have to add one less than n 400-metres to the first 3000. Therefore, for the nth training session:

distance = 3000 + 400(n - 1)

c. If she will run further than a marathon in the kth session, that means she will run more than 42.195 km, which is 42195 metres. Therefore, we can form the following inequality:

3000 + 400(k - 1) > 42195

⇒ 400(k - 1) > 42195 - 3000

⇒ 400(k - 1) > 39195

⇒ k-1 >
`(39195)/(400)`

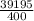
⇒ k - 1 > 97.99

⇒ k > 97.99 + 1

∴k = 99

Therefore, she will run further than a marathon in the 99th training session.