Question

PRE CALCULUS PLEASE HELP ME WITH THESE 2 QUESTIONS

Answer 1

`(51)/(2)`

Explanation:

The value of a definite integral represents the area between the x-axis and the graph of the function you’re integrating between two limits.

`\boxed{\begin{minipage}{8.5 cm}\underline{De\:\!finite integration}\\\\$\displaystyle \int^b_a f(x)\:\:\text{d}x$\\\\\\where $a$ is the lower limit and $b$ is the upper limit.\\\end{minipage}}`

The given definite integral is:

`\displaystyle \int^5_(-7) f(x)\; \;\text{d}x`

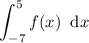
This means we need to find the area between the x-axis and the function between the limits x = -7 and x = 4.

Notice that the function is below the x-axis between x = -7 and x = -2.

Therefore, we need to separate the integral into two areas and add them together:

`\displaystyle \int^5_(-7) f(x)\; \;\text{d}x=\int^(-2)_(-7) f(x)\; \;\text{d}x+\int^5_(-2) f(x)\; \;\text{d}x`

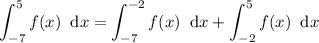
The area between the x-axis and the function between the limits x = -7 and x = -2 is a triangle with base of 5 units and height of 3 units.

The area between the x-axis and the function between the limits x = -2 and x = 5 is a trapezoid with bases of 5 and 7 units, and a height of 3 units.

Using the formulas for the area of a triangle and the area of a trapezoid, the definite integral can be calculated as follows:

`\begin{aligned}\displaystyle \int^5_(-7) f(x)\; \;\text{d}x&=\int^(-2)_(-7) f(x)\; \;\text{d}x+\int^5_(-2) f(x)\; \;\text{d}x\\\\& =(1)/(2)(5)(3)+(1)/(2)(5+7)(3)\\\\& =(15)/(2)+18\\\\& =(51)/(2)\end{aligned}`

Note: If you integrate a function to find an area that lies below the x-axis, it will give a negative value. So when finding an area like this, you will need to make your answer positive, since area cannot be negative.