Question

Find an equation for the tangent to the curve y = 8x x2 1 at the point (1, 4).

Answer 1

The equation of the tangent to the curve y = 8x / (x^2 + 1) at the point (1, 4) is y = -4x + 8.

At the origin (0, 0):

Find the slope of the tangent line:

Differentiate the function
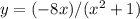`y = (-8x)/(x^2 + 1)` using the quotient rule:

`dy/dx = (-8(x^2 + 1) + 16x^2) / (x^2 + 1)^2 = 8(x^2 - 1) / (x^2 + 1)^2`

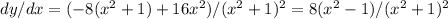
Evaluate the derivative at
`x = 0` (the x-coordinate of the origin):

`dy/dx = 8(0^2 - 1) / (0^2 + 1)^2 = -8`

The slope of the tangent line at the origin is -8.

Use the point-slope form to find the equation of the tangent line:

Point-slope form: y - y1 = m(x - x1)

Plug in the point (0, 0) and the slope -8:

`y - 0 = -8(x - 0) y = -8x`

At the point (-1, 4):

Find the slope of the tangent line:

Evaluate the derivative at x = -1:

`dy/dx = 8((-1)^2 - 1) / ((-1)^2 + 1)^2 = 0`

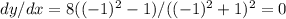
The slope of the tangent line at (-1, 4) is 0.

Use the point-slope form to find the equation of the tangent line:

Plug in the point (-1, 4) and the slope 0:

`y - 4 = 0(x - (-1))\\y - 4 = 0\\y = 4`