To design an op-amp circuit that produces an output voltage
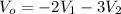 , we can utilize an inverting amplifier configuration. The inverting amplifier has a negative gain, which aligns with the given equation for
, we can utilize an inverting amplifier configuration. The inverting amplifier has a negative gain, which aligns with the given equation for
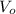 . Here's how you can design the circuit:
. Here's how you can design the circuit:
1. Connect the inverting terminal (marked with a negative sign) of the op-amp to ground (0V).
2. Connect the non-inverting terminal (marked with a positive sign) of the op-amp to the input signal
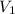 .
.
3. Connect a resistor
 between the inverting terminal and the output terminal of the op-amp.
between the inverting terminal and the output terminal of the op-amp.
4. Connect a resistor
 between the output terminal and the inverting terminal of the op-amp.
between the output terminal and the inverting terminal of the op-amp.
5. Connect the input signal
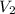 to the junction between
to the junction between
 and
and
 .
.
6. Connect the output terminal of the op-amp to a load or further circuitry, creating
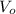 .
.
By applying the voltage divider rule, we can derive the relationship between
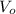 ,
,
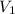 , and
, and
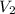 . The voltage at the inverting terminal (
. The voltage at the inverting terminal (
 ) is given by:
) is given by:
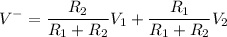
Since the op-amp is assumed to have ideal characteristics (infinite gain), the output voltage
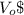 is equal to the voltage at the inverting terminal (
is equal to the voltage at the inverting terminal (
 ) multiplied by the negative gain of the circuit (-2-3 = -5):
) multiplied by the negative gain of the circuit (-2-3 = -5):

Substituting the value of
 , we have:
, we have:

Simplifying this equation, we get:
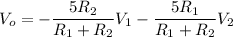
By comparing this equation with the given equation for
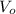 ([-2V₁ -3V2]), we can deduce the values of
([-2V₁ -3V2]), we can deduce the values of
 and
and
 :
:

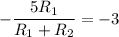
Solving these equations, we find:
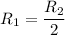
Substituting this value into one of the equations, we can determine
 :
:
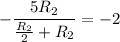
Simplifying:



Hence, the equation doesn't hold true for any value of
 . It seems there is no valid solution to meet the given equation
. It seems there is no valid solution to meet the given equation
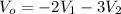 using an inverting amplifier configuration.
using an inverting amplifier configuration.