Question

Compute the fundamental frequency. For non-periodic, the

fundamental value is 10000. x(n) = sin (2n/3)

Answer 1

The given signal is
`\displaystyle x(n) =\sin \left((2n)/(3)\right)`.

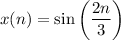To compute the fundamental frequency, we need to find the smallest positive value of
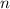`\displaystyle n` for which the sinusoidal function repeats itself. In other words, we are looking for the period of the function.

Since the argument of the sine function is
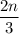`\displaystyle (2n)/(3)`, one complete cycle of the function occurs when
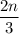`\displaystyle (2n)/(3)` increases by
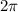`\displaystyle 2\pi`. So, we can set up the equation:

`\displaystyle (2n)/(3) =2\pi`

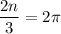
Solving for
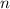`\displaystyle n`, we have:

`\displaystyle n =(3( 2\pi ))/(2) =3\pi`

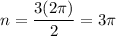
Therefore, the period of the function
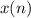`\displaystyle x(n)` is
`\displaystyle 3\pi`. The fundamental frequency is the reciprocal of the period, so:

`\displaystyle \text{{Fundamental frequency}}=(1)/(3\pi )`

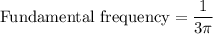
Hence, the fundamental frequency is
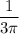`\displaystyle (1)/(3\pi )`.

`\huge{\mathfrak{\colorbox{black}{\textcolor{lime}{I\:hope\:this\:helps\:!\:\:}}}}`

♥️
`\large{\underline{\textcolor{red}{\mathcal{SUMIT\:\:ROY\:\:(:\:\:}}}}`