Question

Solve this ASAP PLS HELP

Answer 1

the solutions x=2, y=-1, (2,-1)

Answer 2

(2, -1)

Explanation:

Given system of equations:

`\begin{cases}y=-2x+3\\y+9=4x\end{cases}`

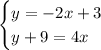
To solve the given system of equations, we can use the method of substitution.

Substitute the first equation into the second equation to eliminate the y term:

`(-2x+3)+9=4x`

Solve for x:

`-2x+3+9=4x`

`-2x+12=4x`

`-2x+12+2x=4x+2x`

`12=6x`

`(12)/(6)=(6x)/(6)`

`2=x`

`x=2`

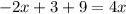
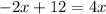
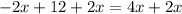
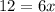
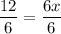
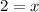
Substitute the found value of x into the first equation and solve for y:

`y=-2(2)+3`

`y=-4+3`

`y=-1`

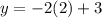
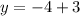
Therefore, the solution to the system of equations is (2, -1).

To verify the solution by graphing the system, find two points on each line by substituting two values of x into each equation. Plot the points and draw a line through them. The solution is the point of intersection.

Graphing y = -2x + 3

`\begin{aligned} x=0 \implies y&=-2(0)+3\\y&=0+3\\y&=3\end{aligned}`
`\begin{aligned} x=-2 \implies y&=-2(-2)+3\\y&=4+3\\y&=7\end{aligned}`

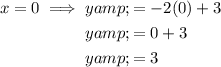
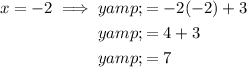
Plot points (0, 3) and (-2, 7) and draw a straight line through them.

Graphing y + 9 = 4x

`\begin{aligned} x=0 \implies y+9&=4(0)\\y+9&=0\\y&=-9\end{aligned}`
`\begin{aligned} x=3 \implies y+9&=4(3)\\y+9&=12\\y&=3\end{aligned}`

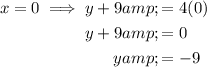
Plot points (0, -9) and (3, 3) and draw a straight line through them.

The solution to the graphed system of equations is the point of intersection of the two lines: (2, 1).