Question

A line segment AB is increased along its length by 25% by producing it to C on the side of B. If A and B have the co-ordinates (1, 2) and (5, 6) respectively then find the co-ordinates of C​

Answer 1

To find the coordinates of point C, we can use the concept of proportionality in the line segment AB.

The proportionality states that if a line segment is increased or decreased by a certain percentage, the coordinates of the new point can be found by extending or reducing the coordinates of the original points by the same percentage.

Given that line segment AB is increased by 25%, we can calculate the change in the x-coordinate and the y-coordinate separately.

Change in x-coordinate:

`\displaystyle \Delta x=25\%\cdot ( 5-1)=0.25\cdot 4=1`

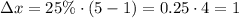
Change in y-coordinate:

`\displaystyle \Delta y=25\%\cdot ( 6-2)=0.25\cdot 4=1`

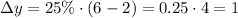
Now, we can add the changes to the coordinates of point B to find the coordinates of point C:

`\displaystyle x_(C) =x_(B) +\Delta x=5+1=6`

`\displaystyle y_(C) =y_(B) +\Delta y=6+1=7`

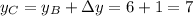
Therefore, the coordinates of point C are
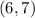`\displaystyle ( 6,7)`.

`\huge{\mathfrak{\colorbox{black}{\textcolor{lime}{I\:hope\:this\:helps\:!\:\:}}}}`

♥️
`\large{\underline{\textcolor{red}{\mathcal{SUMIT\:\:ROY\:\:(:\:\:}}}}`